
分析 根据根与系数的关系即可求得x1+x2与x1•x2的值.
(1)x12+x22=(x1+x2)2-2x1•x2;
(2)$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$.
解答 解:由题意得:x1+x2=-3,x1•x2=-1.
(1)x12+x22=(x1+x2)2-2x1•x2=(-3)2-2×(-1)=9+2=11;
(2)$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{-3}{-1}$=3.
点评 此题考查了根与系数的关系.注意x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,顶角为120°的等腰△ABC的腰长为6,P为底边BC上一点,且BP=2PC,含30°、60°的直角三角板中30°角的顶点落在点P上,三角板绕P点旋转且始终交△ABC的两腰于E、F两点.
如图,顶角为120°的等腰△ABC的腰长为6,P为底边BC上一点,且BP=2PC,含30°、60°的直角三角板中30°角的顶点落在点P上,三角板绕P点旋转且始终交△ABC的两腰于E、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
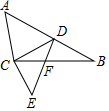 如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且$\frac{CD}{CB}$=$\frac{3}{5}$,$\frac{CE}{AC}$=$\frac{3}{5}$.求证:△ACD∽△ECF.
如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且$\frac{CD}{CB}$=$\frac{3}{5}$,$\frac{CE}{AC}$=$\frac{3}{5}$.求证:△ACD∽△ECF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com