
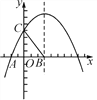
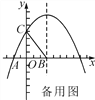
【题目】(本题满分10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标.
【答案】(1) 抛物线的表达式为y=-x2+x+4 ;(2) M的坐标为(6,4)或(3-![]() ,-4)或(3+
,-4)或(3+![]() ,-4).
,-4).
【解析】解:(1)∵抛物线y=ax2+bx+4交x轴于A(-2,0),∴0=4a-2b+4,∵对称轴是直线x=3,∴-![]() =3,即6a+b=0,关于a,b的方程联立解得 a=-,b=,∴抛物线的表达式为y=-x2+x+4 (2)∵四边形为平行四边形,且BC∥MN,∴BC=MN.①N点在M点下方,即M点向下平移4个单位,向右平移3个单位与N重合.设M1(x,- x2+x+4),则N1(x+3,- x2+x),∵N1在x轴上,∴-x2+x=0,解得 x=0(M与C重合,舍去),或x=6,∴xM=6,∴M1(6,4);②M点在N点右下方,即N向下平移4个单位,向右平移3个单位与M重合.设M(x,- x2+x+4),则N(x-3,- x2+x+8),∵N在x轴上,∴-x2+x+8=0,解得 x=3-
=3,即6a+b=0,关于a,b的方程联立解得 a=-,b=,∴抛物线的表达式为y=-x2+x+4 (2)∵四边形为平行四边形,且BC∥MN,∴BC=MN.①N点在M点下方,即M点向下平移4个单位,向右平移3个单位与N重合.设M1(x,- x2+x+4),则N1(x+3,- x2+x),∵N1在x轴上,∴-x2+x=0,解得 x=0(M与C重合,舍去),或x=6,∴xM=6,∴M1(6,4);②M点在N点右下方,即N向下平移4个单位,向右平移3个单位与M重合.设M(x,- x2+x+4),则N(x-3,- x2+x+8),∵N在x轴上,∴-x2+x+8=0,解得 x=3-![]() ,或x=3+
,或x=3+![]() ,∴xM=3-
,∴xM=3-![]() 或3+
或3+![]() .∴M2(3-
.∴M2(3-![]() ,-4)或M3(3+
,-4)或M3(3+![]() ,-4).综上所述,M的坐标为(6,4)或(3-
,-4).综上所述,M的坐标为(6,4)或(3-![]() ,-4)或(3+
,-4)或(3+![]() ,-4)
,-4)


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() 都经过A(1,0),B(﹣2,3)两点.
都经过A(1,0),B(﹣2,3)两点.
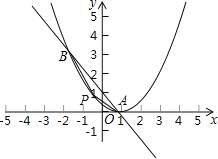
(1)求抛物线y1及直线y2的解析式;
(2)点P是抛物线上一动点,在直线AB的下方,当△PAB的面积最大时,请求出P点坐标;
(3)抛物线上是否存在一点M,使△MAB与△OAB的面积相等?若存在,请求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B'C'的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点 O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com