
【题目】如图①,△ABC中, BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若![]() ,
,![]() ,求∠D的度数;
,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
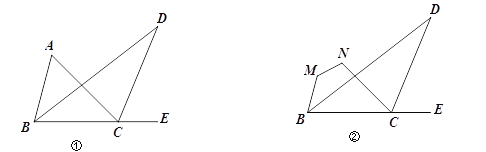
【答案】(1)![]() (2)
(2) ![]() 或写成
或写成![]()
【解析】(1).根据角平分线的定义可得∠DBC=37.5°,根据邻补角定义以及角平分线定义求得∠DCA的度数为67.5°,最后根据三角形内角和定理即可求得∠D的度数;(2).由四边形内角和与角平分线性质即可求解.
本题解析: (1)∵BD平分∠ABC,
∴∠CBD=![]() ∠ABC=
∠ABC=![]() ×75°=37.5°,
×75°=37.5°,
∵CD平分△ABC的外角,
∴∠DCA= ![]() (180°-∠ACB)=
(180°-∠ACB)= ![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠D=180°-∠DBC-∠DCB=180°-37.5°-67.5°-45°=30°;
(2) ∵∠M+∠N+∠CBM+∠NCB=360°,
∴∠D=180°-![]() ∠CBM-∠NCB-
∠CBM-∠NCB-![]() ∠NCE=180°-
∠NCE=180°-![]() (360°-∠NCB-∠M-∠N)- ∠NCB-
(360°-∠NCB-∠M-∠N)- ∠NCB-![]() ∠NCE=180°-180°+
∠NCE=180°-180°+![]() ∠NCB+
∠NCB+![]() ∠M+
∠M+![]() ∠N-∠NCB-
∠N-∠NCB-![]() ∠NCE=
∠NCE=![]() ∠M+
∠M+![]() ∠N-
∠N-![]() ∠NCB-
∠NCB-![]() ∠NCE=
∠NCE=![]() ,或写成
,或写成![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.如果锐角三角形的一个内角是60°,那么这个锐角三角形是等边三角形
B.三角形的角平分线就是三角形内角的平分线
C.直角三角形的斜边的长度大于两条直角边长度的和
D.任何三角形的高必相交于一点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
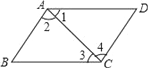
A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
①将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形△A’B’C’;
②画出△DEF关于直线l对称的三角形△D’E’F’;
③填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
利用网格点和三角板画图或计算:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
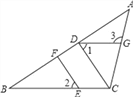
【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
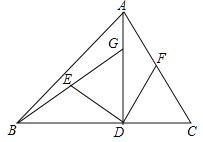
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数分布直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5~80.5分这个分数段;④如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com