分析:(1)EB=DC,理由为:由△ABC与△ADE都是正三角形,利用等边三角形的性质得到AE=AD,AB=AC,且∠EAB=∠DAC=60°,利用SAS得出△AEB与△ADC全等,利用全等三角形的对应边相等即可得证;
(2)∠BDC与∠EBC相等,理由为:由△AEB与△ADC全等得到∠ABE=∠ACD,∠BDC为三角形ADC的外角,利用外角性质得到∠BDC=∠ACD+∠BAC,∠EBC=∠ABE+∠ABC,等量代换即可得证.
解答:解:(1)EB=DC,理由为:
∵△ABC与△ADE都是正三角形,
∴∠EAB=∠DAC=60°,AE=AD,AB=AC,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴EB=DC;
(2)∠EBC=∠BDC,理由为:
∵△AEB≌△ADC,
∴∠ABE=∠ADC,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵∠BDC为△ACD的外角,
∴∠BDC=∠ACD+∠BAC=∠ACD+60°,
∵∠EBC=∠ABE+∠ABC=∠ABE+60°,
∴∠EBC=∠BDC.
点评:此题考查了等边三角形的性质,全等三角形的判定与性质,熟练掌握等边三角形的性质是解本题的关键.

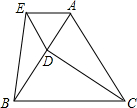 如图,已知△ABC与△ADE都是正三角形.
如图,已知△ABC与△ADE都是正三角形.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案