
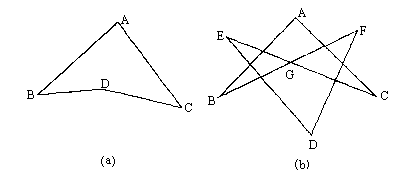
(1)如图(a),求证:∠BDC=∠A+∠B+∠C
(2)如图(b),若∠BGC=![]() ,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
|
答案:解:(1)证法一:如图,延长BD交AC于E, ∵∠BDC=∠DEC+∠C,∠DEC=∠A+∠B ∴∠BDC=∠A+∠B+∠C
证法二:如图,连接AD并延长至E,则∠BDE=∠B+∠BAE,∠CDE=∠C+∠CAE ∴BDE+∠CDE=∠B+∠C+∠BAE+∠CAE 即∠BDC=∠B+∠C+∠A.
证法三:如图,连接BC, ∵∠A+∠ABC+∠ACB=∠D+∠DBC+∠DCD= 即∠A+∠ABD+∠DBC+∠ACD+∠DCB=∠D+∠DBC+∠DCB ∴∠D=∠A+∠ABD+∠ACD 即∠D=∠A+∠B+∠C
(2)由(1)知,在图(b)中,∠BGC=∠A+∠B+∠C ∠EGF=∠D+∠E+∠F ∴∠A+∠B+∠C+∠D+∠E+∠F=∠BGC+∠EGF=2∠BGC=2× 剖析:我们知道,三角形的一个外角等于和它不相邻的两内角之和,这里是求证一个角等于三个角的和,这就启示我们要将此图化为三角形进行研究. |
|
(1)注意学习本题中多种转化的方法;(2)应用所学的知识解题. |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| ||||
| 4 |
| ||||
| 4 |
| ||||
| 4 |
| ||||
| 4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com