
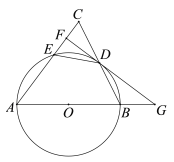
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
(1)求证:GD为⊙O切线;
(2)求证:DE2=EF·AC;
(3)若tan∠C=2,AB=5,求AE的长.
【答案】(1)见解析;(2)见解析;(3)AE=3.
【解析】
(1)欲证明FG是⊙O的切线,只要证明OD⊥FG;
(2) 连接AD,然后求证Rt△CDF∽Rt△CAD,即可解答;
(3)由题意得出∠ABC=∠C,tan∠ABC=tan∠C=![]() ,根据直角三角形的三角函数得出CF=1,即可解答.
,根据直角三角形的三角函数得出CF=1,即可解答.
解:(1)如答图1,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵AB=AC,
∴∠ABC=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DG⊥AC,
∴OD⊥DF,
∴GD为⊙O切线;
(2)如答图2,连接AD,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴CD=BD,∠EAD=∠BAD,
∴BD=DE=CD,
∵DF⊥AC,
∴CF=EF,
∵Rt△CDF∽Rt△CAD,
∴![]() ,即CD2=CF·AC,
,即CD2=CF·AC,
∴DE2=EF·AC;
(3)如答图2,∵AB=AC,
∴∠ABC=∠C,tan∠ABC=tan∠C=![]() ,∵AB=5,
,∵AB=5,
∴BD=DC=![]() ,在Rt△CDF中,
,在Rt△CDF中,
∵tan∠C=2,∴CF=1,由(2)知,,EF=CF,
∴EF=CF=1,CE=2,所以AE=AC-CE=AB-CE=5-2=3.
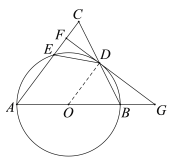
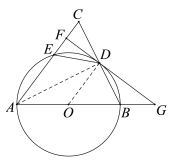
答图1 答图2


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=x+3与x轴、y轴分别交于点A、B,将直线AB向下平移与反比例函数![]() (x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=
(x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=![]() .
.
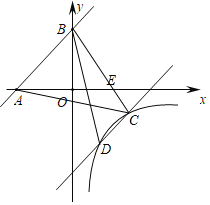
(1)求直线BC和反比例函数解析式;(2)连接BD,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵橘子树,平均每一棵树结
棵橘子树,平均每一棵树结![]() 个橘子.根据经验估计,每多种
个橘子.根据经验估计,每多种![]() 棵树,平均每棵树就会少结
棵树,平均每棵树就会少结![]() 个橘子.设果园增种
个橘子.设果园增种![]() 棵橘子树,果园橘子总个数为
棵橘子树,果园橘子总个数为![]() 个.
个.
(1)根据题意,填写下表:
增种的橘子树(棵) |
|
|
|
| … |
|
平均每棵树结橘子数(个) |
|
(2)求果园里增种多少棵橘子树时,所结橘子总数最多,并求出此时橘子的总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.
与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
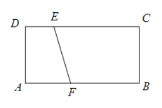
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 公司
公司![]() 年使用自主研发生产的“
年使用自主研发生产的“![]() ”系列甲、乙、丙三类芯片共
”系列甲、乙、丙三类芯片共![]() 万块,生产了
万块,生产了![]() 万部手机,其中乙类芯片的产量是甲类芯片的
万部手机,其中乙类芯片的产量是甲类芯片的![]() 倍,丙类芯片的产量比甲、乙两类芯片产量的和还多
倍,丙类芯片的产量比甲、乙两类芯片产量的和还多![]() 万块.这些“
万块.这些“![]() ”芯片解决了该公司
”芯片解决了该公司![]() 年生产的全部手机所需芯片的
年生产的全部手机所需芯片的![]() .
.
(1)求![]() 年甲类芯片的产量;
年甲类芯片的产量;
(2)![]() 公司计划
公司计划![]() 年生产的手机全部使用自主研发的“
年生产的手机全部使用自主研发的“![]() ”系列芯片.从
”系列芯片.从![]() 年起逐年扩大“
年起逐年扩大“![]() ”芯片的产量,
”芯片的产量,![]() 年、
年、![]() 年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数
年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数![]() ,乙类芯片的产量平均每年增长的百分数比
,乙类芯片的产量平均每年增长的百分数比![]() 小
小![]() ,丙类芯片的产量每年按相同的数量递增.
,丙类芯片的产量每年按相同的数量递增.![]() 年到
年到![]() 年,丙类芯片三年的总产量达到
年,丙类芯片三年的总产量达到![]() 亿块.这样,
亿块.这样,![]() 年的
年的![]() 公司的手机产量比
公司的手机产量比![]() 年全年的手机产量多
年全年的手机产量多![]() ,求丙类芯片
,求丙类芯片![]() 年的产量及
年的产量及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 四点,动点
四点,动点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动(
运动(![]() 不与点
不与点![]() 、点
、点![]() 重合),设运动时间为
重合),设运动时间为![]() (秒).
(秒).
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 在(
在(![]() )中的抛物线上,当
)中的抛物线上,当![]()
![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)当![]() 在
在![]() 上运动时,如图②.过点
上运动时,如图②.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(4)点![]() 为
为![]() 轴上一点,直线
轴上一点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,直接写出符合条件的所有
为等腰三角形?若存在,直接写出符合条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
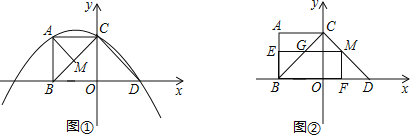
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
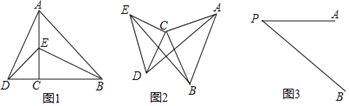
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
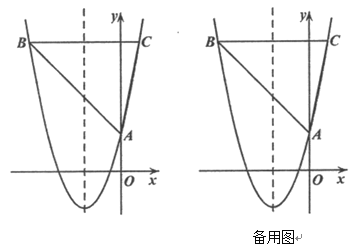
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,平行于
,平行于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在对称轴左侧,
在对称轴左侧,![]() .
.
I.求此抛物线的解析式;
Ⅱ.已知在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 的周长最小,求点
的周长最小,求点![]() 的坐标;
的坐标;
Ⅲ.若过点![]() 的直线
的直线![]() 将
将![]() 的面积分成2:3两部分,试求直线
的面积分成2:3两部分,试求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com