
分析 ①利用根的判别式△>0判定即可;
②根据向左平移横坐标减求出平移前的点的坐标,然后代入函数解析式计算即可求出m的值;
③根据二次函数的对称性求出对称轴,即可求出m的值.
解答 解:①∵△=(-2m)2-4×1×(-3)=4m2+12>0,
∴它的图象与x轴有两个公共点,故本小题正确;
②∵将它的图象向左平移3个单位后过原点,
∴平移前的图象经过点(3,0),
代入函数关系式得,32-2m•3-3=0,
解得m=1,故本小题正确;
③∵当x=2时的函数值与x=8时的函数值相等,
∴对称轴为直线x=$\frac{2+8}{2}$=5,
∴-$\frac{-2m}{2×1}$=5,
解得m=5,故本小题正确;
综上所述,结论正确的是①②③共2个.
故答案为:①②③.
点评 本题考查了二次函数图象,二次函数的性质,主要利用了二次函数与x轴的交点问题,二次函数的对称性以及增减性,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
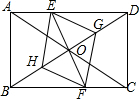 如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.
如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
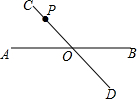 如图,直线AB、CD相交于O,P是CD上一点按要求画图并回答问题:
如图,直线AB、CD相交于O,P是CD上一点按要求画图并回答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com