
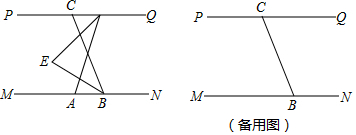
分析 (1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分两种情形讨论即可解决问题.
解答 解:(1)如图1中,延长DE交MN于H.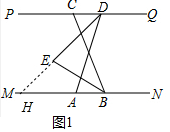
∵∠ADQ=110°,ED平分∠ADP,
∴∠PDH=$\frac{1}{2}$∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB平分∠ABC,
∴∠EBH=$\frac{1}{2}$∠ABC=30°,
∴∠BED=∠EHB+∠EBH=75°.
(2)有两种情形,如图2中,当n>60°.延长DE交MN于H.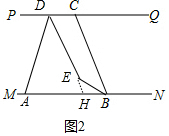
∵PQ∥MN,
∴∠QDH=∠DHB=$\frac{1}{2}$n,
∴∠BED=∠EHB+∠EBH=($\frac{1}{2}$n)°+30°,
当n<60°,如图3中,设BE交PQ于H.
∵∠DHB=∠HBA=30°,∠EDH=($\frac{1}{2}$n)°,
又∵∠DHB=∠BED+∠EDH,
∴∠BED=30°-($\frac{1}{2}$n)°,
当n=60°,∠BED不存在.
综上所述,∠BED=($\frac{1}{2}$n)°+30°或30°-($\frac{1}{2}$n)°.
点评 本题考查平行线的性质、角平分线的定义、三角形的外角的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
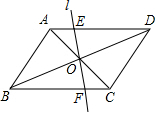 在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.
在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
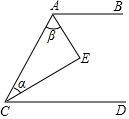 请将下列证明过程补充完整:
请将下列证明过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 甲 | 87 | 95 | 85 | 93 |
| 乙 | 80 | 80 | 90 | 90 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com