
 如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H
如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H分析 将△ADF绕点A顺时针旋转90°得到△ABG,根据旋转的性质可得DF=BG,AF=AG,∠DAF=∠BAG,然后求出∠EAF=∠EAG=45°,再利用“边角边”证明△AEF和△AEG全等,根据全等三角形对应边上的高相等可得AH=AB.
解答 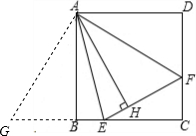 证明:将△ADF绕点A顺时针旋转90°得到△ABG,
证明:将△ADF绕点A顺时针旋转90°得到△ABG,
由旋转的性质得,DF=BG,AF=AG,∠DAF=∠BAG.
∵∠FAG=∠BAG+∠BAF=∠DAF+∠BAF=∠BAD=90°,
∠EAF=45°,
∴∠EAF=∠EAG=45°.
在△AEF和△AEG中,
$\left\{\begin{array}{l}{AF=AG}\\{∠EAF=∠EAG}\\{AE=AE}\end{array}\right.$,
∴△AEF≌△AEG(SAS),
∵AH、AB分别是△AEF和△AEG对应边上的高,
∴AH=AB.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质,全等三角形的判定与性质,利用旋转作辅助线构造出全等三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
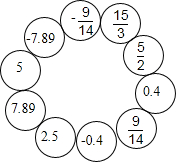 某天,黄新同学遇到了一个这样的涂色游戏:如图,把每一对互为相反数所在的色框涂上你喜欢的不同颜色;绝对值为5的数所在的色框涂上蓝色;到数轴原点距离为2.5的数所在的色框涂上黑色,感兴趣的你赶快试试吧!
某天,黄新同学遇到了一个这样的涂色游戏:如图,把每一对互为相反数所在的色框涂上你喜欢的不同颜色;绝对值为5的数所在的色框涂上蓝色;到数轴原点距离为2.5的数所在的色框涂上黑色,感兴趣的你赶快试试吧!查看答案和解析>>
科目:初中数学 来源: 题型:解答题
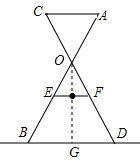 如图,小红家阳台上放置了一个晒衣架,如图是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面上,AC∥BD.现将晒衣架完全稳固张开,扣链EF成一条直线,过O作OG⊥BD于G,经测量:OA=OB,OG=48cm.小红的连衣裙挂在衣架上后的总长度达到100cm,则垂挂在晒衣架上后是否会拖落到地面?请通过计算说明.
如图,小红家阳台上放置了一个晒衣架,如图是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面上,AC∥BD.现将晒衣架完全稳固张开,扣链EF成一条直线,过O作OG⊥BD于G,经测量:OA=OB,OG=48cm.小红的连衣裙挂在衣架上后的总长度达到100cm,则垂挂在晒衣架上后是否会拖落到地面?请通过计算说明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
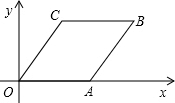 如图,?OABC的顶点O、A、C的坐标分别是(0,0),(2,0),(0.5,1),则点B的坐标是( )
如图,?OABC的顶点O、A、C的坐标分别是(0,0),(2,0),(0.5,1),则点B的坐标是( )| A. | (1,2) | B. | (0.5,2) | C. | (2.5,1) | D. | (2,0.5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
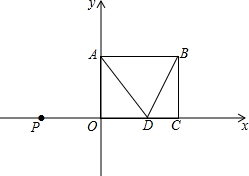 如图,在平面直角坐标系中,点B的坐标为(10,8),过点B分别作BA⊥y轴,BC⊥x轴,垂足分别为A,C,在OC上取一点D,连接AD,BD,使得AD=AB,现有一动点P从点O出发,沿x轴负方向以每秒2个单位长度的速度运动,设点P的运动时间为t秒.
如图,在平面直角坐标系中,点B的坐标为(10,8),过点B分别作BA⊥y轴,BC⊥x轴,垂足分别为A,C,在OC上取一点D,连接AD,BD,使得AD=AB,现有一动点P从点O出发,沿x轴负方向以每秒2个单位长度的速度运动,设点P的运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com