练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图1，抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$与x轴交于A、B两点（点A在点B的左侧），交y轴于点C．连接AC，过点A作AC的垂线交抛物线的对称轴于点D．

    （1）求点D的坐标；
    （2）点P为直线AD下方抛物线上一动点，当△PAD面积最大时，作PE⊥x轴于点E，连接AP，点M、N分别为线段AP、AE上的两个动点，求EM+MN的最小值；
    （3）如图2，抛物线的顶点为点Q，平移抛物线，使抛物线的顶点Q在直线AQ上移动，点A、Q平移后的对应点分别为点A′、Q′．在平面内有一动点G，当以点A′，Q′，B，G为顶点的四边形为平行四边形时，找出满足条件的所有点G为顶点的多边形是轴对称图形时，点Q′的坐标．

    分析 （1）首先求出A、B、C的坐标，在Rt△ADH中，由∠DAH=30°，AH=2，求出DH即可解决问题．
    （2）如图2中，过点A作y轴的平行线，过点D作x轴的平行线，两直线交于点G，易知G（-1，$\frac{2\sqrt{3}}{3}$），设P（m，$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$），根据S△PAD=S△AGP+S△DGP-S△AGD构建二次函数，利用二次函数的性质求出点P以及点E的坐标，如图3中，E（$\frac{3}{2}$，0），作等E关于直线PA的对称点E′，EE′交AP于K，作EN⊥x轴于N，交AP于M，连接EM，根据此线段最短可知，此时EM+MN最短，最小值=E′M+MN=E′N，求出点E′的坐标即可解决问题．
    （3）如图4中，由题意，Q（1，-$\frac{4\sqrt{3}}{3}$），作BH⊥AQ于H，求得点H坐标（$\frac{5}{7}$，-$\frac{8\sqrt{3}}{7}$），首先判断点G的位置，根据轴对称图形的性质，判断出点Q的位置，一一求解即可．

    解答 解：（1）如图1中，设对称轴交AB于H．

    对于抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$令x=0得y=-$\sqrt{3}$；令y=0得$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$=0解得x=-1或3，
    ∴C（0，-$\sqrt{3}$），A（-1，0），B（3，0），
    ∴OA=1，OC=$\sqrt{3}$，
    ∴tan∠OAC=$\frac{OC}{OA}$=$\sqrt{3}$，
    ∴∠OAC=60°，
    ∵AD⊥AC，
    ∴∠DAC=90°，∠DAH=30°，
    ∵抛物线的对称轴x=-$\frac{b}{2a}$=1，
    ∴AH=2，DH=AH•tan30°=$\frac{2\sqrt{3}}{3}$，
    ∴D（1，$\frac{2\sqrt{3}}{3}$）．

    （2）如图2中，过点A作y轴的平行线，过点D作x轴的平行线，两直线交于点G，易知G（-1，$\frac{2\sqrt{3}}{3}$），设P（m，$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$），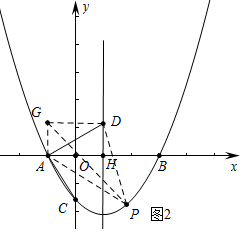

    ∵S△PAD=S△AGP+S△DGP-S△AGD
    =$\frac{1}{2}$•$\frac{2\sqrt{3}}{3}$•（1+m）+$\frac{1}{2}$•2•（$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$）-$\frac{1}{2}$•2•$\frac{2\sqrt{3}}{3}$
    =-$\frac{\sqrt{3}}{3}$（m-$\frac{3}{2}$）2+$\frac{25\sqrt{3}}{12}$．
    ∵-$\frac{\sqrt{3}}{3}$＜0，
    ∴m=$\frac{3}{2}$时，△PAD的面积最大，此时P（$\frac{3}{2}$，-$\frac{5}{4}$$\sqrt{3}$），
    如图3中，E（$\frac{3}{2}$，0），作等E关于直线PA的对称点E′，EE′交AP于K，

    ∵直线PA的解析式为y=-$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{3}}{2}$，直线EE′的解析式为y=$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$，
    由$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{2}x-\frac{\sqrt{3}}{2}}\\{y=\frac{2\sqrt{3}}{3}x-\sqrt{3}}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=\frac{3}{7}}\\{y=-\frac{5}{7}\sqrt{3}}\end{array}\right.$，
    ∴点K的坐标（$\frac{3}{7}$，-$\frac{5}{7}$$\sqrt{3}$），
    ∵EK=KE′，
    ∴E′（-$\frac{9}{14}$，-$\frac{10}{7}$$\sqrt{3}$）
    作EN⊥x轴于N，交AP于M，连接EM，
    根据此线段最短可知，此时EM+MN最短，最小值=E′M+MN=E′N=$\frac{10\sqrt{3}}{7}$．

    （3）如图4中，BG1=BG2=AQ，且BG1∥AQ，G1、G2是满足条件的点，

    当A1Q1为平行四边形的对角线时，点G的轨迹是图中的直线，
    当BG3⊥AQ时，得Q1满足条件，
    当G4G2⊥AQ时，得Q2满足条件，
    当G5G1⊥AQ时，得Q3满足条件，
    当G3G2=G1G2时，G3G2交AQ于Q4，Q4满足条件，
    当G1G3=G1G2时，G3G1与AQ的交于点Q5，Q5也满足条件，
    由题意，Q（1，-$\frac{4\sqrt{3}}{3}$），以点A′，Q′，B，G为顶点的四边形必须是矩形或菱形，
    ∴直线AQ的解析式为y=-$\frac{2\sqrt{3}}{3}$x-$\frac{2\sqrt{3}}{3}$，作BH⊥AQ于H，
    可得直线BH的解析式为y=$\frac{\sqrt{3}}{2}$x-$\frac{3\sqrt{3}}{2}$，
    由$\left\{\begin{array}{l}{y=-\frac{2\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}}\\{y=\frac{\sqrt{3}}{2}x-\frac{3\sqrt{3}}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{5}{7}}\\{y=-\frac{8\sqrt{3}}{7}}\end{array}\right.$，
    ∴点H坐标（$\frac{5}{7}$，-$\frac{8\sqrt{3}}{7}$），
    易知Q1（$\frac{12}{7}$，-$\frac{38}{21}$$\sqrt{3}$），Q2（$\frac{19}{7}$，-$\frac{24}{7}$$\sqrt{3}$），Q3（-$\frac{9}{7}$，0），Q4（$\frac{17}{7}$，-$\frac{16}{7}$$\sqrt{3}$），Q5（1，-$\frac{4}{3}$$\sqrt{3}$）．

    综上所述，满足条件的点Q′的坐标Q1（$\frac{12}{7}$，-$\frac{38}{21}$$\sqrt{3}$），Q2（$\frac{19}{7}$，-$\frac{24}{7}$$\sqrt{3}$），Q3（-$\frac{9}{7}$，0），Q4（$\frac{17}{7}$，-$\frac{16}{7}$$\sqrt{3}$），Q5（1，-$\frac{4}{3}$$\sqrt{3}$）．

    点评 本题考查二次函数综合题、一次函数的应用、锐角三角函数、垂线段最短、平行四边形的性质、矩形的性质等知识，解题的关键是学会构建二次函数解决最值问题，学会利用垂线段最短解决最短问题，学会寻找特殊点解决实际问题，属于中考压轴题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A（-4，2）、B（n，-4）两点．
    （1）求上述反比例函数和一次函数的解析式；
    （2）求△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列方程一定是一元二次方程的是（　　）
    A．ax2+bx+c=0B．2x2-3=2（x+1）2C．（a2+1）x2=0D．$\frac{1}{x}$=x-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．数学活动--“关于三角形全等的条件”
    【问题提出】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
    【初步思考】我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
    【逐步探究】
    （1）第一种情况：当∠B是直角时，如图①，根据HL定理，可得△ABC≌△DEF．
    （2）第二种情况：当∠B是钝角时，△ABC≌△DEF仍成立．请你完成证明．
    已知：如图②，△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，
    求证：△ABC≌△DEF．
    （3）第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
    在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
    【深入思考】
    ∠B还要满足什么条件，就可以使△ABC≌△DEF？（请直接写出结论．）
    在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若∠B≥∠A，则△ABC≌△DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知：如图，在?ABCD中，AD＞AB，∠ABC的平分线交AD于点E，EF∥AB交BC于点F．四边形ABFE是菱形吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知：如图，在△ABC中，AD平分∠BAC．
    （1）作线段AD的垂直平分线MN，MN与AB边交于点E，AC边交于点F．
    （2）若AB=AC，请直接写出EF和BC的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，AB∥DE，∠α：∠D：∠B=2：3：4，求∠α．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，△ABC中，AB=AC，D是AB的中点，AD=5cm，DE⊥AB于D交AC于E，△EBC的周长是24cm，则BC=（　　）cm．
    A．29B．19C．14D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题，请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程的长．
    （1）如图1，正方体的棱长为5cm，一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处；
    （2）如图2，长方体底面是边长为5cm的正方形，高为6cm，一只蚂蚁欲从长方体底面上的点A沿长方体表面爬到点C1处．

    查看答案和解析>>

    同步练习册答案