
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点的坐标分别为A(-2,0),B(-4,4),C(3,-3).
(1)画出△ABC;
(2)画出△ABC向右平移3个单位长度,再向上平移4个单位长度后得到的△A1B1C1;
(3)求出△A1B1C1的面积.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB= ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 . 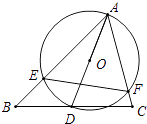
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是一个聪明而又富有想象力的孩子.学习了“有理数的乘方”后,他就琢磨着使用“乘方”这一数学知识脑洞大开地定义出“有理数的除方”概念.于是规定:若干个相同有理数(均不能为0)的除法运算叫做除方,如5÷5÷5,(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)等,类比有理数的乘方.小明把5÷5÷5记作f(3,5),(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)记作f(4,﹣2)
(1)直接写出计算结果,f(5,![]() )= ,f(6,3)= ;
)= ,f(6,3)= ;
(2)关于“有理数的除方”下列说法正确的是 (填序号)
①对于任何正整数n,都有f(n,﹣1)=1;
②f(6,3)=f(3,6);
③f(2,a)=1(a≠0);
④对于任何正整数n,都有f(2n,a)<0(a<0).
(3)小明深入思考后发现:“除方”运算能够转化成乘方运算,且结果可以写成幂的形式.请推导出“除方”的运算公式f(n,a)(n为正整数,a≠0,n≥2),要求写出推导过程将结果写成幂的形式(结果用含a,n的式子表示)
(4)请利用(3)问的推导公式计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?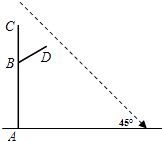
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进西装30件,衬衫45件,共用了39000元,其中西装的单价是衬衫的5倍。
(1)求西装和衬衫的单价各为多少元?
(2)商场仍需要购买上面的两种产品55件(每种产品的单价不变),采购部预算共支出32000元,财会算了一下,说:“如果你用这些钱共买这两种产品,那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com