
【题目】(2016广东省梅州市第22题)
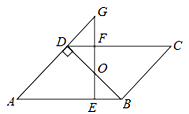
如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【答案】(1)、证明过程见解析;(2)、AE=3.
【解析】
试题分析:(1)、根据平行四边形的性质得出∠OBE =∠ODF,从而得出△OBE和△ODF全等,从而得出答案;(2)、根据EF⊥AB,AB ∥DC得出∠GEA=∠GFD=90°,根据∠A的度数得出AE=GE,根据垂直得出OF=FG=1,根据三角形全等得出OE=OF=1,从而根据GE=OE+OF+FG得出答案.
试题解析:(1)、∵四边形ABCD是平行四边形, ∴DC∥AB ∴∠OBE =∠ODF.
在△OBE与△ODF中, ∵ 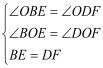 ∴△OBE≌△ODF(AAS) ∴BO=DO
∴△OBE≌△ODF(AAS) ∴BO=DO
(2)、∵EF⊥AB,AB ∥DC, ∴∠GEA=∠GFD=90° ∵∠A=45°, ∴∠G=∠A=45°
∴AE=GE ∵BD⊥AD, ∴∠ADB=∠GDO=90° ∴∠GOD=∠G=45° ∴DG=DO
∴OF=FG= 1 由(1)可知,OE=OF=1 ∴GE=OE+OF+FG=3 ∴AE=3


科目:初中数学 来源: 题型:
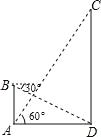
【题目】(2016广东省茂名市第21题)如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
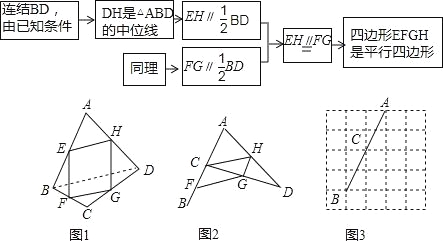
【题目】(2016浙江省舟山市第22题)如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
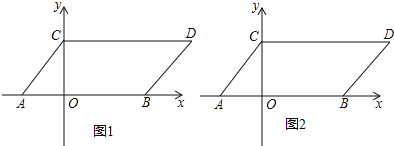
(1)写出点C,D的坐标并求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由;
(3)如图2,点P是直线BD上的一个动点,连接PC,PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD,∠POB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
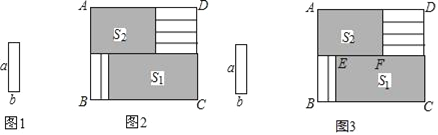
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=_________,S2=_________;
(2)求a,b满足的关系式,写出推导过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com