
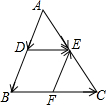
 如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )| A. | $\overrightarrow{DE}$∥$\overrightarrow{BC}$ | B. | $\overrightarrow{AD}-\overrightarrow{AE}=\overrightarrow{DE}$ | C. | $\overrightarrow{DB}$=$-\overrightarrow{FE}$ | D. | $\overrightarrow{DB}+\overrightarrow{DE}+\overrightarrow{FE}=\overrightarrow{DE}$ |
分析 根据三角形法则,结合图形,即可判断出不正确的选项.
解答 解:∵点D、E、F分别是AB、AC、BC的中点,
∴DE∥BC,
∴$\overrightarrow{DE}$∥$\overrightarrow{BC}$,A选项正确;
$\overrightarrow{AD}$-$\overrightarrow{AE}$=$\overrightarrow{ED}$,B选项错误;
$\overrightarrow{DB}$=-$\overrightarrow{FE}$,C选项正确;
$\overrightarrow{DB}$+$\overrightarrow{DE}$+$\overrightarrow{FE}$=$\overrightarrow{DE}$,D选项正确;
故选B.
点评 本题主要考查了平面向量以及三角形中位线定量的知识,解题的关键是掌握向量的运算法则,此题难度不大.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 王师傅 | +8 | +6 | -2 | 0 | +6 | -3 | +5 | +7 | -5 | +9 |
| 刘师傅 | +6 | +3 | -6 | +3 | -3 | -4 | -7 | 0 | -4 | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )
如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )| A. | 2cm | B. | 3cm | C. | $\sqrt{3}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )
如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )| A. | 四边形AFCE是平行四边形 | B. | 四边形AFCE是菱形 | ||
| C. | 四边形ABCF是等腰梯形 | D. | 四边形AECD是等腰梯形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形ABCD中,AC∥BD,AB=13cm,AC=14cm,CD=15cm,BD=28cm.在直线BD上,动点P从B点出发向右运动,同时,另一个动点Q从D点出发向左运动.
在四边形ABCD中,AC∥BD,AB=13cm,AC=14cm,CD=15cm,BD=28cm.在直线BD上,动点P从B点出发向右运动,同时,另一个动点Q从D点出发向左运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com