
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.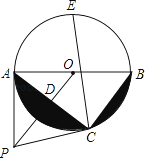
(1)求证:PC是⊙O的切线;
(2)若PD=![]() ,AC=8,求图中阴影部分的面积;
,AC=8,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
【答案】
(1)
证明:如图1,连接OC,
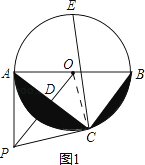
∵PA切⊙O于点A,∴∠PAO=90°,
∵BC∥OP,
∴∠AOP=∠OBC,∠COP=∠OCB,
∵OC=OB,∴∠OBC=∠OCB,
∴∠AOP=∠COP,
在△PAO和△PCO中,
 ,
,
∴△PAO≌△PCO,
∴∠PCO=∠PAO=90°,
∴PC是⊙O的切线;
(2)
解:由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90°,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD=∠AOD,
∴△ADP∽△ODA,
∴![]() ,
,
∴AD2=PDDO,
∵AC=8,PD=![]() ,
,
∴AD=![]() AC=4,OD=3,AO=5,
AC=4,OD=3,AO=5,
由题意知OD为△的中位线,
∴BC=6,OD=6,AB=10.
∴S阴=![]() S⊙O﹣S△ABC=
S⊙O﹣S△ABC=![]() ﹣24;
﹣24;
(3)
解:如图2,
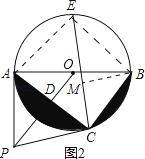
连接AE、BE,作BM⊥CE于M,
∴∠CMB=∠EMB=∠AEB=90°,
∵点E是![]() 的中点,
的中点,
∴∠ECB=∠CBM=∠ABE=45°,
CM=MB=3![]() ,
,
BE=ABcos45°=5![]() ,
,
∴EM=![]() =4
=4![]() ,
,
则CE=CM+EM=7![]() .
.
【解析】(1)连接OC,证明△PAO≌△PCO,得到∠PCO=∠PAO=90°,证明结论;
(2)证明△ADP∽△PDA,得到成比例线段求出BC的长,根据S阴=S⊙O﹣S△ABC求出答案;
(3)连接AE、BE,作BM⊥CE于M,分别求出CM和EM的长,求和得到答案.
此题考查了圆的综合应用,涉及知识点有全等三角形的判定及性质,相似三角形的性质,割补法求阴影部分面积,勾股定理的应用.


科目:初中数学 来源: 题型:
【题目】如图1,直线l交x轴于点C,交y轴于点D,与反比例函数y= ![]() (k>0)的图象交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3
(k>0)的图象交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3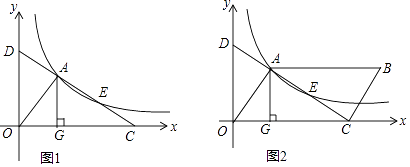
(1)k=;
(2)求证:AD=CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径 ![]() ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( ) 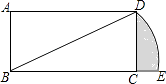
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 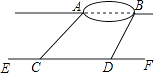
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An﹣1为OA的n等分点,B1、B2、B3、…Bn﹣1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An﹣1Bn﹣1 , 分别交![]() (x≥0)于点C1、C2、C3、…、Cn﹣1 , 当B25C25=8C25A25时,则n= .
(x≥0)于点C1、C2、C3、…、Cn﹣1 , 当B25C25=8C25A25时,则n= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.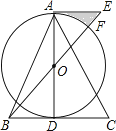
(1)求证:AE是⊙O的切线;
(2)若BD=![]() AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )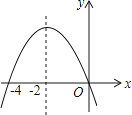
A.①③④
B.②④⑤
C.①②⑤
D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图:
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,比赛成绩达到90分以上(含90分)的为优秀作品,据此估计该校参赛作品中,优秀作品有多少份?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com