

| A. | 8$\sqrt{2}$ | B. | 12 | C. | 4$\sqrt{2}$ | D. | 6 |
分析 根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,当直线经过D点,设交AB与N,则DN=4,作DM⊥AB于点M.利用三角函数即可求得DM,即平行四边形的高,然后利用平行四边形的面积公式即可求解.
解答  解:解据图象可以得到当移动的距离是4时,直线经过点A,
解:解据图象可以得到当移动的距离是4时,直线经过点A,
当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,
当直线经过D点,设交AB与N,则DN=4,
作DM⊥AB于点M.
∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DNM=45°,
∴DM=DN•sin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
∴平行四边形的面积=AB•DM=4×2$\sqrt{2}$=8$\sqrt{2}$.
故选:A.
点评 本题考查了函数的图象,根据图象理解AB的长度,运用解直角三角形求得平行四边形的高是解决问题的关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
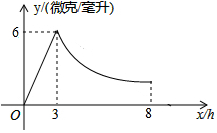 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.
某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 机场 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A机场 | 15 | 20 |
| B机场 | 10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
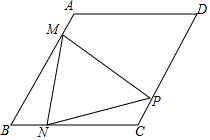 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com