
【题目】 正方形![]() 的边长为1,点
的边长为1,点![]() 是
是![]() 边上的一个动点(与
边上的一个动点(与![]() 不重合),以
不重合),以![]() 为顶点在
为顶点在![]() 所在直线的上方作
所在直线的上方作![]() .
.
(1)当![]() 经过点
经过点![]() 时,
时,
①请直接填空:![]() (可能,不可能)过
(可能,不可能)过![]() 点;(图1仅供分析)
点;(图1仅供分析)
②如图2,在![]() 上截取
上截取![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,册
,册![]() 于
于![]() ,求证:四边形
,求证:四边形![]() 为正方形.
为正方形.
(2)当![]() 不过点
不过点![]() 时,设
时,设![]() 交边
交边![]() 于
于![]() ,且
,且![]() .在
.在![]() 上存在点
上存在点![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,使得
,使得![]() ,连接
,连接![]() ,求四边形
,求四边形![]() 的最大面积.
的最大面积.

【答案】(1)①不可能②证明见解析(2)![]()
【解析】
试题分析:(1)①若ON过点D时,则在△OAD中不满足勾股定理,可知不可能过D点;
②由条件可先判业四边形EFCH为矩形,再证明△OFE≌△ABO,可证得结论;
(2)由条件可证明△PKO∽△OBG,利用相似三角形的性质可求得OP=2,可求得△POG面积为定值及△PKO和△OBG的关系,只要△CGB的面积有最大值时,则四边形PKBG的面积就最大,设OB=a,BG=b,由勾股定理可用b表示出a,则可用a表示出△CBG的面积,利用二次函数的性质可求得其最大值,则可求得四边形PKBG面积的最大值.
试题解析: (1)①若ON过点D,则OA>AB,OD>CD,
∴OA2>AD2,OD2>AD2,
∴OA2+OD2>2AD2≠AD2,
∴∠AOD≠90°,这与∠MON=90°矛盾,
∴ON不可能过D点,
故答案为:不可能;
②∵EH⊥CD,EF⊥BC,
∴∠EHC=∠EFC=90°,且∠HCF=90°,
∴四边形EFCH为矩形,
∵∠MON=90°,
∴∠EOF=90°﹣∠AOB,
在正方形ABCD中,∠BAO=90°﹣∠AOB,
∴∠EOF=∠BAO,
在△OFE和△ABO中
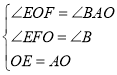
∴△OFE≌△ABO(AAS),
∴EF=OB,OF=AB,
又OF=CF+OC=AB=BC=BO+OC=EF+OC,
∴CF=EF,
∴四边形EFCH为正方形;
(2)∵∠POK=∠OGB,∠PKO=∠OBG,
∴△PKO∽△OBG,
∵S△PKO=4S△OBG,
∴![]() =(
=(![]() )2=4,
)2=4,
∴OP=2,
∴S△POG=![]() OGOP=
OGOP=![]() ×1×2=1,
×1×2=1,

设OB=a,BG=b,则a2+b2=OG2=1,
∴b=![]() ,
,
∴S△OBG=![]() ab=
ab=![]() a
a![]() =
=![]()
![]() =
=![]()
![]() ,
,
∴当a2=![]() 时,△OBG有最大值
时,△OBG有最大值![]() ,此时S△PKO=4S△OBG=1,
,此时S△PKO=4S△OBG=1,
∴四边形PKBG的最大面积为1+1+![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用2种方法表示可得一个等式,求等式。
(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.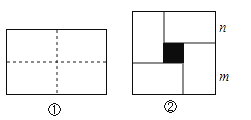
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)直接写出关于![]() 的一元二次方程
的一元二次方程![]() 的一个根;
的一个根;
(2)证明:抛物线![]() 的顶点
的顶点![]() 在第三象限;
在第三象限;
(3)直线![]() 与
与![]() 轴分别相交于
轴分别相交于![]() 两点,与抛物线
两点,与抛物线![]() 相交于
相交于![]() 两点.设抛物线
两点.设抛物线![]() 的对称轴与
的对称轴与![]() 轴相交于
轴相交于![]() ,如果在对称轴左侧的抛物线上存在点
,如果在对称轴左侧的抛物线上存在点![]() ,使得
,使得![]() 与
与![]() 相似.并且
相似.并且![]() ,求此时抛物线的表达式.
,求此时抛物线的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x+2交y轴于点A1 , 在x轴正方向上取点B1 , 使OB1=0A1;过点B1作A2B1⊥x轴,交l于点A2 , 在x轴正方向上取点B2 , 使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3 , 在x轴正方向上取点B3 , 使B2B3=B2A3记△OA1B1面积为S1,△B1A2B2面积为S2 , △B2A3B3面积为S3 , …则S2018等于.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD四个顶点的坐标分别是A(1,2![]() ),B(4,2
),B(4,2![]() ),C(4,
),C(4, ![]() ),D(1,
),D(1, ![]() ).
).

(1)求这个长方形的面积;
(2)将这个长方形向下平移2![]() 个单位长度,再向右平移1个单位长度,得到长方形A′B′C′D′,求长方形A′B′C′D′四个顶点的坐标.
个单位长度,再向右平移1个单位长度,得到长方形A′B′C′D′,求长方形A′B′C′D′四个顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com