
【题目】如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD于点E,AD=12 cm,AB=7 cm,求DE的长度.
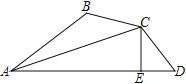
【答案】2.5cm
【解析】
过C作CF⊥AB的延长线于点F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件∠ABC+∠D=180°,由△FBC≌△EDC,由全等的性质可得BF=ED,问题可得解.
证明:如图,
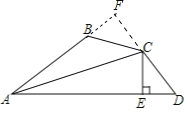
过C作CF⊥AB的延长线于点F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AD,CF⊥AB,
∴∠BFC=∠CED=90°,
在△AFC和△AEC中,
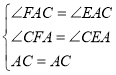
∴△AFC≌△AEC,
∴AF=AE,CF=CE,
∵∠ABC+∠D=180°,∠ABC+∠FBC=180°,
∴∠FBC=∠EDC,
∴△FBC≌△EDC,
∴BF=ED,
∴AB+AD=AE+ED+AF-BF=2AE,
∵AD=12cm,AB=7cm,
∴19=2AE,
∴AE=9.5cm,
∴DE=AD-AE=12-9.5=2.5cm.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=60°,BE=2cm,DF=3cm,试求平行四边形ABCD的周长及面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段叫做这个三角形的“等角分割线”.
例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”.

(1)如图1,在△ABC中,D是边BC上一点,若∠B=30°,∠BAD=∠C=40°,求证: AD为△ABC的“等角分割线”;
(2)如图2,△ABC中,∠C=90°,∠B=30°;
①画出△ABC的“等角分割线”,写出画法并说明理由;
②若BC=3,求出①中画出的“等角分割线”的长度.
(3)在△ABC中,∠A=24°,若△ABC存在“等角分割线”CD,直接写出所有符合要求的∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△在ABC中,∠C=90°,∠B=30°,以A为圆心、任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,给出下列说法:①DM=DN;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3,其中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,给出下列说法:①DM=DN;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3,其中正确的个数是( )
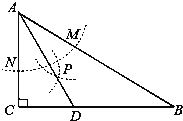
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市绿化部门决定利用现有的不同种类花卉搭配园艺造型,摆放于城区主要大道的两侧.A、B两种园艺造型均需用到杜鹃花,A种造型每个需用杜鹃花25盆,B种造型每个需用杜鹃花35盆,解答下列问题:
(1)已知人民大道两侧搭配的A、B两种园艺造型共60个,恰好用了1700盆杜鹃花,A、B两种园艺造型各搭配了多少个?
(2)如果搭配一个A种造型的成本W与造型个数![]() 的关系式为:W=100―
的关系式为:W=100―![]() x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.

(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
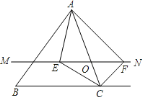
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上(端点除外)的一个动点,过点
边上(端点除外)的一个动点,过点![]() 作直线
作直线![]() .设
.设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,连接
,连接![]() 、
、![]() .那么当点
.那么当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
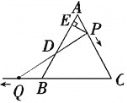
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com