
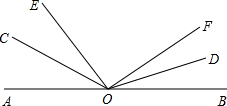
 喜羊羊、美羊羊在微信建立了一个学习讨论组,现在他们讨论了一道关于角的和与差的题,如图.
喜羊羊、美羊羊在微信建立了一个学习讨论组,现在他们讨论了一道关于角的和与差的题,如图.分析 (1)根据邻补角的概念得出∠BOE的度数,再根据角平分线定义和角的之间关系解答即可;
(2)根据邻补角的概念得出∠AOE+∠BOF的度数,再根据角平分线定义和角的之间关系解答即可.
解答 解:(1)∵OC是∠AOE的平分线,∠AOC=26°
∴∠AOE=52°,
∴∠BOE=180°-52°=128°,
∴∠EOD=∠BOE-∠BOD=128°-10°=118°;
(2)∵∠EOF=98°
∴∠AOE+∠BOF=180°-98°=102°,
∵OC是∠AOE的平分线,OD是∠BOF的平分线,
∴∠COE+∠FOD=$\frac{1}{2}$(∠AOE+∠BOF)=51°,
∴∠COD=∠EOF+∠COE+∠FOD=98°+51°=149°.
点评 此题主要考查了邻补角、角平分线的性质,关键是掌握邻补角互补.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,边长AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P.
如图,在正方形ABCD中,边长AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
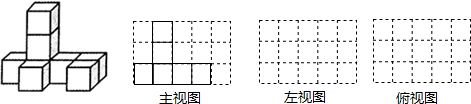

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,下列说法:(1)四边形AEDF是平行四边形;(2)若∠BAC=90°,则四边形AEDF是矩形;(3)若AD平分∠BAC,则四边形AEDF是菱形;(4)若AD⊥BC且AB=AC,则四边形AEDF是正方形.其中正确的是(1)(2)(3).(只填正确答案的序号).
如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,下列说法:(1)四边形AEDF是平行四边形;(2)若∠BAC=90°,则四边形AEDF是矩形;(3)若AD平分∠BAC,则四边形AEDF是菱形;(4)若AD⊥BC且AB=AC,则四边形AEDF是正方形.其中正确的是(1)(2)(3).(只填正确答案的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com