
分析 设平移后抛物线的解析式为y=(x+h)2+k.则易求线段AB的长度,结合三角形的面积公式来求h的值.
解答  解:设平移后抛物线的解析式为y=(x-h)2+k=x2-2xh+h2+k,A(x1,y1),B(x2,y2),
解:设平移后抛物线的解析式为y=(x-h)2+k=x2-2xh+h2+k,A(x1,y1),B(x2,y2),
∵新的抛物线与y轴交于点Q(0,-3),
∴h2+k=-3,P(h,k),
又∵x1+x2=2h,x1•x2=h2+k=-3,
∴AB=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{4{h}^{2}-4{h}^{2}-4k}$=2$\sqrt{-k}$,
∴$\frac{1}{2}$×2$\sqrt{-k}$×|k|=8,
解得k=-4,
∴h2-4=-3,则h=±1.
故该抛物线的解析式分为:y=(x±1)2-4,对称轴为x=±1.
点评 本题考查了二次函数图象与几何变换.解答过程中,要注意k<0.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c图象如图所示,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图所示,下列正确的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
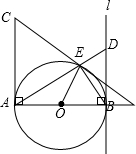 如图,AB=AC=8,∠BAC=90°,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连接DA交⊙O于点E.
如图,AB=AC=8,∠BAC=90°,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连接DA交⊙O于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com