
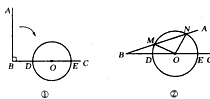
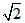 ,求弧MN的长。
,求弧MN的长。|
解:(1)当射线BA绕点B按顺时针方向旋转60°或120°时与⊙O相切, |
 |
(2)∵MN=2 ,OM=ON=2 ,OM=ON=2∴MN2=OM2+ON2,∴∠MON=90° ∴弧MN的长为l=90π×2/180=π。 |
 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、如图,在△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,
20、如图,在△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,查看答案和解析>>
科目:初中数学 来源: 题型:
 8、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
8、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com