
【题目】已知:在![]() 中,
中,![]() ,
,![]() 的高
的高![]() 、
、![]() 交于点
交于点![]() .
.
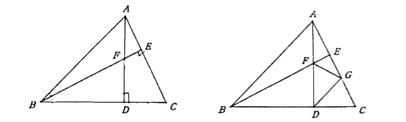
(1)求证:![]() .
.
(2)过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)根据已知条件易证∠DBF=∠DAC,BD=AD,∠BDF=∠ADC, 再利用ASA得到△ADC与△BDF全等;
(2)由DG//AB可得∠BAD=∠FDG=45°,可得:∠GDC =∠FDG=45°,根据SAS可证![]() 可得∠DGF =∠DCG,即可得出结论.
可得∠DGF =∠DCG,即可得出结论.
解:(1)∵AD、BE为△ABC的高,
∴∠ADB=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∵∠ABC=45°,∠ADB=90°,
∴∠DAB=45°,
∴∠ABD=∠BAD,
∴AD=BD,
在△BDF和△ADC中,
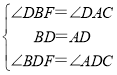 ,
,
∴△BDF≌△ADC(ASA),
(2)∵∠DAB=45°,DG//AB
∴∠BAD=∠FDG=45°
∴∠GDC=90°-∠FDG=45°
∴∠GDC =∠FDG=45°
又∵FD=CD,DG=DG
∴![]()
∴∠DGF =∠DCG
∵△BDF≌△ADC
∴∠BFD=∠ACD
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() 、
、![]() 各点的坐标分别为
各点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.

(1)在给出的图形中,画出四边形![]() 关于
关于![]() 轴对称的四边形
轴对称的四边形![]() ,并写出点
,并写出点![]() 和
和![]() 的坐标;
的坐标;
(2)在四边形![]() 内部画一条线段将四边形分割成两个等腰三角形,并直接写出两个等腰三角形的面积差.
内部画一条线段将四边形分割成两个等腰三角形,并直接写出两个等腰三角形的面积差.
查看答案和解析>>
科目:初中数学 来源: 题型:
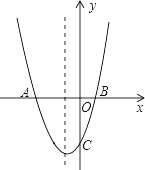
【题目】如图,已知:二次函数y=x2+bx+c 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与 y 轴交于点 C(0,-3)在抛物线上.
(1)求抛物线的表达式;
(2)抛物线的对称轴上有一动点 P,求出当 PB+PC 最小时点 P的坐标;
(3)若抛物线上有一动点Q,使△ABQ的面积为6,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=![]() ,那么这个三角形的面积S=
,那么这个三角形的面积S=![]() .这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
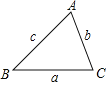
如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1 +h2的值
查看答案和解析>>
科目:初中数学 来源: 题型:
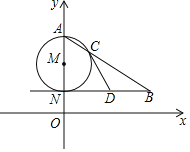
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)若CD ﹦6, AC ﹦8,求⊙O的半径
(2)求证:CF﹦BF;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com