
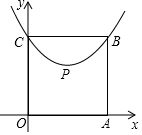
 【定义表述】我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,例如点P(2,4)的特征线有:x=2,y=4,y=x+2,y=-x+6
【定义表述】我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,例如点P(2,4)的特征线有:x=2,y=4,y=x+2,y=-x+6分析 【定义理解】根据一个点的“特征线”的定义即可求出点P(a,b)(a≠b)所有的特征线;
【定义应用】(1)根据y=$\frac{2}{9}$(x-m)2+n得出顶点P(m,n),点C(0,$\frac{2}{9}{m}^{2}+n$),由点P有一条特征线是x=3得到m=3,根据抛物线的对称性得出BC=6,由正方形的性质得出OC=BC=6,根据C点纵坐标为6得出$\frac{2}{9}$×32+n=6,求出n=4,即可求得此抛物线对应的函数表达式;
(2)作点B关于直线y=x+1的对称点B′,连结AB′交直线y=x+1于点Q,如图①,则此时AQ+BQ的值最小,最小值为AB′的长;
(3)分两种情形①当点A′落在直线x=3上时,如图②,②当点A′落在直线y=4上时,如图③,分别求出直线OM的解析式,求出直线OM与对称轴的交点坐标即可解决问题;
解答 解:【定义理解】
∵在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,
∴点P(a,b)(a≠b)所有的特征线为:x=a,y=b,y=x-a+b,y=-x+a+b;
【定义应用】
(1)∵抛物线y=$\frac{2}{9}$(x-m)2+n的顶点为P,与y轴交于点C,
∴点P的坐标为:(m,n),点C的坐标为:(0,$\frac{2}{9}{m}^{2}+n$),
∵点P有一条特征线是x=3,
∴m=3,
∵点B、C均在抛物线上,
∴BC=3×2=6,
∵四边形OABC为正方形,
∴OC=BC=6,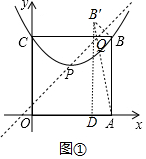
∴$\frac{2}{9}$×32+n=6,解得:n=4,
∴此抛物线对应的函数表达式为:y=$\frac{2}{9}$(x-3)2+4;
(2)由(1)可知,点Q在与一、三象限角平分线平行的点P的特征线为y=x+1.
作点B关于直线y=x+1的对称点B′,连结AB′交直线y=x+1于点Q,如图①,则此时AQ+BQ的值最小.
过点B′作B′D⊥x轴于点D,则BB′=$\sqrt{2}$,B′D=1+6=7,DA=1.
∵在Rt△AB′D中,∠ADB′=90°,
∴AB′=$\sqrt{A{D}^{2}+B′{D}^{2}}$=$\sqrt{{1}^{2}+{7}^{2}}$=5$\sqrt{2}$,
∴AQ+BQ的最小值为5$\sqrt{2}$;
(3)①当点A′落在直线x=3上时,如图②.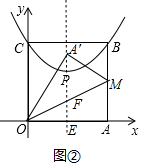
设直线x=3与x轴交于点E,与OM交于点F,则有OA′=OA=6,OE=3,∠A′OM=∠AOM,
在Rt△A′OE中,∠A′EO=90°,cos∠A′OE=$\frac{OE}{OA′}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴∠A′OE=60°,
∴∠AOM=$\frac{1}{2}$∠A′OE=$\frac{1}{2}$×60°=30°,
∴EF=OE•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴当抛物线顶点落在OM上的平移距离为4-$\sqrt{3}$.
②当点A′落在直线y=4上时,如图③,
设直线y=4与y轴交于点G,与AB交于点H.
则有OA′=OA=6,OG=AH=4,且△GOA′≌△HA′M,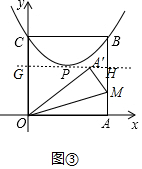
∴$\frac{A′G}{HM}$=$\frac{OG}{A′H}$,
在Rt△A′GO中,∠A′GO=90°,
A′G=$\sqrt{OA{′}^{2}-O{G}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴A′H=GH-A′G=6-2$\sqrt{5}$,
∴$\frac{2\sqrt{5}}{4-AM}$=$\frac{4}{6-2\sqrt{5}}$,
∴AM=9-3$\sqrt{5}$,
∴直线OM的解析式为y=$\frac{3-\sqrt{5}}{2}$x,
当x=3时,y=$\frac{3-\sqrt{5}}{2}$×3=$\frac{9-3\sqrt{5}}{2}$,
∴当抛物线顶点落在OM上的平移距离为4-$\frac{9-3\sqrt{5}}{2}$=$\frac{3\sqrt{5}-1}{2}$,
∴当抛物线顶点落在OM上的平移距离为4-$\sqrt{3}$或$\frac{3\sqrt{5}-1}{2}$.
点评 本题考查二次函数综合题、翻折变换、正方形的性质、勾股定理、一次函数的应用、轴对称最短问题等知识,解题的关键是理解题意,学会利用对称解决最短问题,学会用分类讨论的思想思考问题,学会构建一次函数解决交点坐标问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 3.12×105 | B. | 3.12×106 | C. | 31.2×105 | D. | 0.312×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
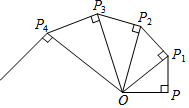 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2017=$\sqrt{2018}$.
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2017=$\sqrt{2018}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com