练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在下列情况下，可解的直角三角形是( )

    A.已知b=3，∠C=90°B.已知∠C=90°,∠B=46°

    C.已知a=3,b=6,∠C=90°D.已知∠B=15°,∠A=65°

    【答案】C

    【解析】

    要解直角三角形，必须求出直角三角形的三个内角和三边长.

    A项中，缺少∠A或∠B的值，故不能解直角三角形；

    B项中，知道角的关系，但是没有边的大小，故不能解直角三角形；

    C项中，利用勾股定理求出c的值，然后利用锐角三角函数的定义求出∠A和∠B.

    D项中，∠C=100°，不是直角三角形.

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明每天从家去学校上学行走的路程为900米，某天他从家去上学时以每分30米的速度行走了450米，为了不迟到他加快了速度，以每分45米的速度行走完剩下的路程，设该天小明上学行走t分时行走的路程为S米，则当l5＜t≤25时，s与t之间的函数关系是（　　）
    A.s=30t
    B.s=900-30t
    C.S=45t-225
    D.s=45t-675

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若二次函数y=(1-k)x2-2x-1的图象与x轴有2个交点，则k的取值范围是_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角三角形中，两个锐角的度数比为2：3，则较小锐角的度数为（　　）
    A.20°
    B.32°
    C.36°
    D.72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等腰△ABC中，AB=AC，则有BC边上的中线，高线和∠BAC的平分线重合于AD（如图一）．若将等腰△ABC的顶点A向右平行移动后，得到△A′BC（如图二），那么，此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 ， ， ．（填A′D、A′E、A′F）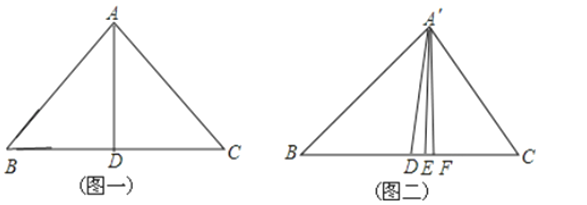

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，长方形OABC中，O为平面直角坐标系的原点，点A、C的坐标分别为A（3，0），C（0，2），点B在第一象限．
    （1）写出点B的坐标；
    （2）若过点C的直线交长方形的OA边于点D，且把长方形OABC的周长分成2：3的两部分，求点D的坐标；
    （3）如果将（2）中的线段CD向下平移3个单位长度，得到对应线段C′D′，在平面直角坐标系中画出△CD′C′，并求出它的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（4，0）及在第一象限的动点P（x ， y），且x+y=6，O为坐标原点，设△OPA的面积为S ．
    （1）求S关于x的函数解析式；
    （2）求x的取值范围；
    （3）当S=6时，求P点坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．得平行四边形ABDC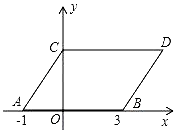

    （1）直接写出点C，D的坐标；
    （2）若在y轴上存在点 M，连接MA，MB，使S△MAB=S平行四边形ABDC ， 求出点M的坐标．
    （3）若点P在直线BD上运动，连接PC，PO．
    请画出图形，直接写出∠CPO、∠DCP、∠BOP的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx+b（k≠0）图象过点（0，2），且与两坐标轴围成的三角形面积为2，则一次函数的解析式为（　　）.
    A.y=x+2
    B.y=-x+2
    C.y=x+2或y=-x+2
    D.y=-x+2或y=x-2

    查看答案和解析>>

    同步练习册答案