
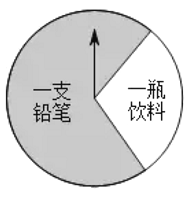
°æƒø°øƒ≥…Ã≥°”–“ª∏ˆø…“‘◊‘”…◊™∂صƒ‘≤–Œ◊™≈Ã(»ÁÕº).πÊ∂®£∫πÀøÕπ∫ŒÔ![]() ‘™“‘…œø…“‘ªÒµ√“ª¥Œ◊™∂Ø◊™ ≈õƒª˙ª·£¨µ±◊™≈ÃÕ£÷π ±÷∏’ά‰‘⁄ƒƒ“ª∏ˆ«¯”ÚæÕªÒµ√œý”¶µƒΩ±∆∑ (÷∏’Î÷∏œÚ¡Ω∏ˆ…»–ŒµƒΩªœþ ±£¨µ±◊˜÷∏œÚ”“±þµƒ…»–Œ)£¨œ¬±Ì «ªÓ∂ØΩ¯––÷–µƒ“ª◊ÈÕ≥º∆ ˝æð£∫
‘™“‘…œø…“‘ªÒµ√“ª¥Œ◊™∂Ø◊™ ≈õƒª˙ª·£¨µ±◊™≈ÃÕ£÷π ±÷∏’ά‰‘⁄ƒƒ“ª∏ˆ«¯”ÚæÕªÒµ√œý”¶µƒΩ±∆∑ (÷∏’Î÷∏œÚ¡Ω∏ˆ…»–ŒµƒΩªœþ ±£¨µ±◊˜÷∏œÚ”“±þµƒ…»–Œ)£¨œ¬±Ì «ªÓ∂ØΩ¯––÷–µƒ“ª◊ÈÕ≥º∆ ˝æð£∫
◊™∂Ø◊™≈õƒ¥Œ ˝ |
|
|
|
|
|
|
¬‰‘⁄°∞«¶± "µƒ¥Œ ˝ |
|
|
|
|
|
|
¬‰‘⁄°∞«¶± "µƒ∆µ¬ |
|
|
|
|
|
|
£®1£©◊™∂Ø∏√◊™≈Óª¥Œ£¨ªÒµ√«¶± µƒ∏≈¬ ‘ºŒ™____ £ª( Ω·π˚±£¡Ù–° ˝µ„∫Û“ªŒª ˝◊÷)£ª
£®2£©«¶± √ø÷ª![]() ‘™£¨“˚¡œ√ø∆ø
‘™£¨“˚¡œ√ø∆ø![]() ‘™£¨æ≠Õ≥º∆∏√…Ã≥°√øÃÏ‘º”–
‘™£¨æ≠Õ≥º∆∏√…Ã≥°√øÃÏ‘º”–![]() √˚πÀ∏˜≤Œº”≥ÈΩ±ªÓ∂Ø£¨«Îº∆À„∏√…Ã≥°√øÃÏ–Ë“™÷ß≥ˆµƒΩ±∆∑∑—”√£ª
√˚πÀ∏˜≤Œº”≥ÈΩ±ªÓ∂Ø£¨«Îº∆À„∏√…Ã≥°√øÃÏ–Ë“™÷ß≥ˆµƒΩ±∆∑∑—”√£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨∏√…Ã≥°œÎ∞—√øÃÏ÷ß≥ˆµƒΩ±∆∑∑—”√øÿ÷∆‘⁄![]() ‘™◊Û”“£¨‘Ú◊™≈Ã…œ°∞“ª∆ø“˚¡œ°±«¯”Úµƒ‘≤–ƒΩ«”¶µ˜’˚Œ™ ∂»£Æ
‘™◊Û”“£¨‘Ú◊™≈Ã…œ°∞“ª∆ø“˚¡œ°±«¯”Úµƒ‘≤–ƒΩ«”¶µ˜’˚Œ™ ∂»£Æ
°æ¥∞∏°ø(1)0.7£ª(2)∏√…Ã≥°√øÃÏ¥Û÷¬–Ë“™÷ß≥ˆ![]() ‘™Ω±∆∑∑—”√£∫(3)36
‘™Ω±∆∑∑—”√£∫(3)36
°æΩ‚Œˆ°ø
£®1£©¿˚”√∆µ¬ π¿º∆∏≈¬ º¥ø…«ÛΩ‚£ª
£®2£©∏˘æð…»–ŒÕ≥º∆Õº£¨Ω·∫œªÒµ√«¶± µƒ∏≈¬ Œ™0.7£¨«Û≥ˆªÒµ√“ª∆ø“˚¡œµƒ∏≈¬ Œ™0.3£¨¡–≥ˆÀ„ Ω40000°¡0.7°¡0.5+40000°¡0.3°¡3£¨º∆À„º¥ø…«ÛΩ‚£ª
£®3£©…Ë◊™≈Ã…œ°∞“ª∆ø“˚¡œ°±«¯”Úµƒ‘≤–ƒΩ«”¶µ˜’˚Œ™n°„£¨‘Ú![]() £¨Ω‚∑Ω≥ú¥ø…£Æ
£¨Ω‚∑Ω≥ú¥ø…£Æ
Ω‚£∫£®1£©◊™∂Ø∏√◊™≈Óª¥Œ£¨ªÒµ√«¶± µƒ∏≈¬ ‘ºŒ™0.7£ª
£®2£©1-0.7=0.3£¨40000°¡0.7°¡0.5+40000°¡0.3°¡3=14000+36000=50000‘™£ª
£®3£©…Ë◊™≈Ã…œ°∞“ª∆ø“˚¡œ°±«¯”Úµƒ‘≤–ƒΩ«”¶µ˜’˚Œ™n°„£¨
‘Ú![]() £¨
£¨
Ω‚∑Ω≥õ√£∫n=36£Æ


 ≥§Ω≠◊˜“µ±æÕ¨≤Ω¡∑œ∞≤·œµ¡–¥∞∏
≥§Ω≠◊˜“µ±æÕ¨≤Ω¡∑œ∞≤·œµ¡–¥∞∏ –°ÃÏ≤≈øŒ ±◊˜“µœµ¡–¥∞∏
–°ÃÏ≤≈øŒ ±◊˜“µœµ¡–¥∞∏ “ªøŒÀƒ¡∑œµ¡–¥∞∏
“ªøŒÀƒ¡∑œµ¡–¥∞∏ ª∆∏‘–°◊¥‘™¬˙∑÷≥¥Ì¢≤‚—Èœµ¡–¥∞∏
ª∆∏‘–°◊¥‘™¬˙∑÷≥¥Ì¢≤‚—Èœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ‚≤ªµ» Ω◊È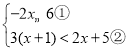 «ÎΩ·∫œÃ‚“‚ÃÓø’£¨ÕÍ≥…±æµƒΩ‚¥£Æ
«ÎΩ·∫œÃ‚“‚ÃÓø’£¨ÕÍ≥…±æµƒΩ‚¥£Æ
£®¢Ò£©Ω‚≤ªµ» Ω¢Ÿ£¨µ√°° °°£ª
£®¢Ú£©Ω‚≤ªµ» Ω¢⁄£¨µ√°° °°£ª
£®¢Û£©∞—≤ªµ» Ω¢Ÿ∫Õ¢⁄µƒΩ◊º∂‘⁄ ˝÷·…œ±Ì æ≥ˆ¿¥£ª
£®¢Ù£©‘≠≤ªµ» Ω◊ȵƒΩ‚ºØŒ™°° °°
![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() £¨
£¨![]() ¡Ωµ„£®
¡Ωµ„£®![]() µ„Œª”⁄
µ„Œª”⁄![]() µ„◊Û≤ý£©£¨”Î
µ„◊Û≤ý£©£¨”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() µ„£¨¡¨Ω”
µ„£¨¡¨Ω”![]() £Æµ„
£Æµ„![]() Œ™≈◊ŒÔœþµƒ∂•µ„£¨µ„
Œ™≈◊ŒÔœþµƒ∂•µ„£¨µ„![]() Œ™
Œ™![]() £Æ
£Æ

£®1£©µ„![]() «µ⁄ÀƒœÛœÞƒ⁄≈◊ŒÔœþ…œµƒ“ªµ„£¨π˝µ„
«µ⁄ÀƒœÛœÞƒ⁄≈◊ŒÔœþ…œµƒ“ªµ„£¨π˝µ„![]() ◊˜
◊˜![]() ÷·Ωª≈◊ŒÔœþ”⁄µ„
÷·Ωª≈◊ŒÔœþ”⁄µ„![]() £¨◊˜
£¨◊˜![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨◊˜
£¨◊˜![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨µ„
£¨µ„![]() ‘⁄µ„
‘⁄µ„![]() ”“±þ£Æµ„
”“±þ£Æµ„![]() «÷±œþ
«÷±œþ![]() …œ“ª∏ˆ∂ص„£¨µ„
…œ“ª∏ˆ∂ص„£¨µ„![]() «÷±œþ
«÷±œþ![]() …œ“ª∏ˆ∂ص„£¨µ±Àƒ±þ–Œ
…œ“ª∏ˆ∂ص„£¨µ±Àƒ±þ–Œ![]() µƒ÷Ð≥§◊Ó¥Û ±£¨«Û
µƒ÷Ð≥§◊Ó¥Û ±£¨«Û![]() µƒ◊Ó–°÷µ£ª
µƒ◊Ó–°÷µ£ª
£®2£©»ÁÕº2£¨Ω´‘≠≈◊ŒÔœþ»∆∆‰∂‘≥∆÷·”Î![]() ÷·µƒΩªµ„
÷·µƒΩªµ„![]() –˝◊™
–˝◊™![]() µ√–¬µƒ≈◊ŒÔœþ
µ√–¬µƒ≈◊ŒÔœþ![]() £¨µ„
£¨µ„![]() £¨
£¨![]() µƒ∂‘”¶µ„∑÷±º«Œ™
µƒ∂‘”¶µ„∑÷±º«Œ™![]() £¨
£¨![]() £¨∞—≈◊ŒÔœþ
£¨∞—≈◊ŒÔœþ![]() —ÿ÷±œþ
—ÿ÷±œþ![]() ∆Ω“∆£¨
∆Ω“∆£¨![]() £¨
£¨![]() µƒ∂‘”¶µ„∑÷±º«Œ™
µƒ∂‘”¶µ„∑÷±º«Œ™![]() £¨
£¨![]() «∑ҥʑ⁄µ„
«∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() «“‘
«“‘![]() Œ™—¸µƒµ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆ
Œ™—¸µƒµ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆ![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
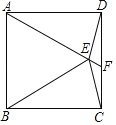
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–ŒABCD÷–£¨°˜ABEŒ™µ»±þ»˝Ω«–Œ£¨¡¨Ω”DE£¨CE£¨—”≥§AEΩªCD”⁄Fµ„£¨‘Ú°œDEFµƒ∂» ˝Œ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
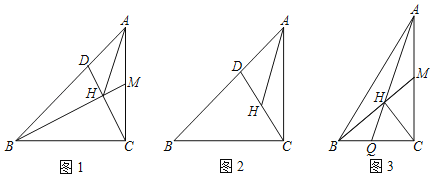
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨![]() =n£¨MŒ™BC…œµƒ“ªµ„£¨¡¨Ω”BM£Æ
=n£¨MŒ™BC…œµƒ“ªµ„£¨¡¨Ω”BM£Æ
£®1£©»ÁÕº1£¨»Ùn=1£¨
¢Ÿµ±MŒ™ACµƒ÷–µ„£¨µ±BM°ÕCD”⁄H£¨¡¨Ω”AH£¨«Û°œAHDµƒ∂» ˝£ª
¢⁄»ÁÕº2£¨µ±HŒ™CDµƒ÷–µ„£¨°œAHD=45°„£¨«Û![]() µƒ÷µ∫Õ°œCAHµƒ∂» ˝£ª
µƒ÷µ∫Õ°œCAHµƒ∂» ˝£ª
£®2£©»ÁÕº3£¨CH°ÕAM”⁄H£¨¡¨Ω”CH≤¢—”≥§ΩªAC”⁄Q£¨MŒ™AC÷–µ„£¨÷±Ω”–¥≥ˆtan°œBHQµƒ÷µ£®”√∫¨nµƒ Ω◊”±Ì 棩£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþy=![]() x2+bx+cæ≠π˝°˜ABCµƒ»˝∏ˆ∂•µ„£¨∆‰÷–µ„A£®0£¨1£©£¨µ„B£®©Å9£¨10£©£¨AC°Œx÷·£¨µ„P ±÷±œþACœ¬∑Ω≈◊ŒÔœþ…œµƒ∂ص„£Æ
x2+bx+cæ≠π˝°˜ABCµƒ»˝∏ˆ∂•µ„£¨∆‰÷–µ„A£®0£¨1£©£¨µ„B£®©Å9£¨10£©£¨AC°Œx÷·£¨µ„P ±÷±œþACœ¬∑Ω≈◊ŒÔœþ…œµƒ∂ص„£Æ

£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª£®2£©π˝µ„P«“”Îy÷·∆Ω––µƒ÷±œþl”Î÷±œþAB°¢AC∑÷±Ωª”⁄µ„E°¢F£¨µ±Àƒ±þ–ŒAECPµƒ√ʪ˝◊Ó¥Û ±£¨«Ûµ„Pµƒ◊¯±Í£ª
£®3£©µ±µ„PŒ™≈◊ŒÔœþµƒ∂•µ„ ±£¨‘⁄÷±œþAC…œ «∑ҥʑ⁄µ„Q£¨ πµ√“‘C°¢P°¢QŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜ABCœýÀ∆£¨»Ù¥Ê‘⁄£¨«Û≥ˆµ„Qµƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™Àƒ±þ–ŒABDE «∆Ω––Àƒ±þ–Œ£¨CŒ™±þB D—”≥§œþ…œ“ªµ„£¨¡¨Ω·AC°¢CE£¨ πAB=AC£Æ
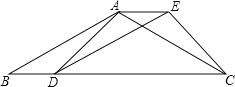
£®1£©«Û÷§£∫°˜BAD°’°˜AEC£ª
£®2£©»Ù°œB=30°„£¨°œADC=45°„£¨BD=10£¨«Û∆Ω––Àƒ±þ–ŒABDEµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC‘⁄÷±Ω«◊¯±Íœµ÷–
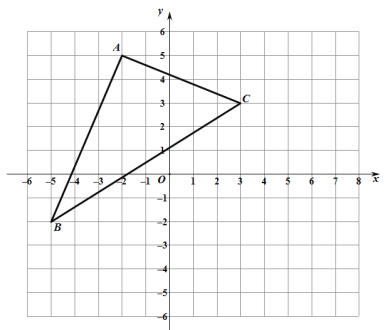
£®1£©«Î–¥≥ˆ°˜ABC∏˜µ„µƒ◊¯±Í£ª
£®2£©«Û≥ˆ°˜ABCµƒ√ʪ˝£ª
£®3£©»ÁÕº£¨Ω´»˝Ω«–ŒABCœÚ”“∆Ω“∆3∏ˆµ•Œª≥§∂»£¨‘ŸœÚœ¬∆Ω“∆2∏ˆµ•Œª≥§∂»£¨µ√µΩ∂‘”¶µƒ»˝Ω«–ŒA1B1C1£¨≤¢–¥≥ˆµ„A1°¢B1°¢C1µƒ◊¯±Í
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com