
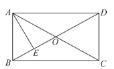
【题目】如图,在矩形ABCD中,AE⊥BD,垂足为点E,若BE=OE=1 cm,则∠AOB=______,S矩形ABCD=_______.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB⊥MN,CD⊥MN,垂足分别为B,D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
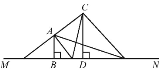
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
(1)实践操作:![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作
点作![]() ,与直线
,与直线![]() 相交于点
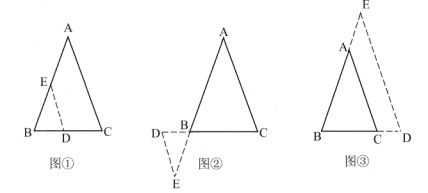
相交于点![]() ,如图①,图②,图③所示,则
,如图①,图②,图③所示,则![]() 的形状为______.
的形状为______.
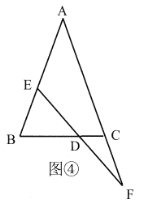
(2)问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
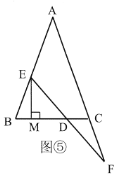
(3)拓展与应用,在(2)的条件下,如图⑤,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
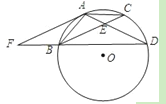
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com