

分析 (1)根据了解很少的人数和所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角
的度数;
(2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图;
(3)根据题意先画出树状图,再根据概率公式即可得出答案.
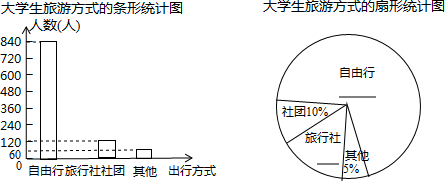
解答 解:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人).
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:$\frac{15}{60}$×360°=90°.
故答案为:60,90;
(2)了解的人数有:60-15-30-10=5(人),补图如下: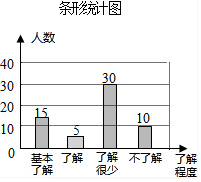
(3)画树状图得: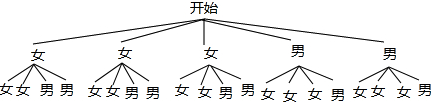
∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,
∴恰好抽到1个男生和1个女生的概率为:$\frac{12}{20}$=$\frac{3}{5}$.
点评 此题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率,读懂题意,根据题意求出总人数是解题的关键;概率=所求情况数与总情况数之比.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
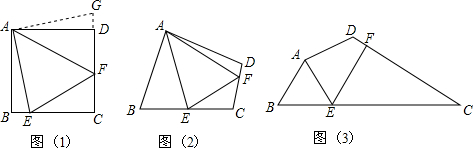
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
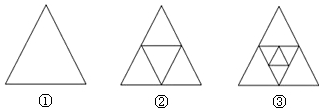
| A. | 33个 | B. | 36个 | C. | 37个 | D. | 41个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
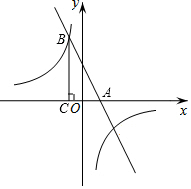 如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).
如图,在平面直角坐标系xOy中,直线y=kx+3(k≠0)与x轴交于点A,与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为B(-1,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
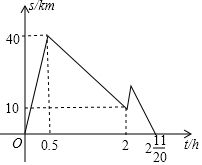 甲、乙两辆汽车同时从A地出发前往相距250千米的B地,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到B地,如图是甲、乙两车之间的距离s(km2),乙车出发时间t(h)之间的函数关系图象,则甲车比乙车早到11.5分钟.
甲、乙两辆汽车同时从A地出发前往相距250千米的B地,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到B地,如图是甲、乙两车之间的距离s(km2),乙车出发时间t(h)之间的函数关系图象,则甲车比乙车早到11.5分钟.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com