
分析 首先在同一平面直角坐标系中画出函数y=|x+1|与y=|2x-3|的图象,设两图象交于点A、B,分别求出A、B两点的坐标,再观察图象,函数y=|x+1|落在y=|2x-3|的图象下方的部分对应的x的取值范围即为所求.
解答  解:如图,在同一平面直角坐标系中画出函数y=|x+1|与y=|2x-3|的图象,两图象交于点A、B.
解:如图,在同一平面直角坐标系中画出函数y=|x+1|与y=|2x-3|的图象,两图象交于点A、B.
如果x+1=2x-3,x=4,A点坐标为(4,5),
如果x+1=3-2x,x=$\frac{2}{3}$,B点坐标为($\frac{2}{3}$,$\frac{5}{3}$).
由图象可知,当x<$\frac{2}{3}$或x>4时,函数y=|x+1|的图象在y=|2x-3|图象的下方,即|x+1|<|2x-3|,
所以|x+1|-|2x-3|<0的解集为x<$\frac{2}{3}$或x>4.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.准确画出两个函数的图象是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 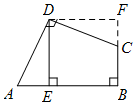 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
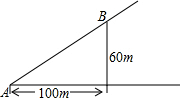 如图,有一个山坡,如果沿山坡在水平AC方向上每前进100m铅直高度就升高60m,那么用科学计算器求坡角∠A的度数,并以“度、分、秒”为单位表示出这个度数,下列按键顺序正确的是( )
如图,有一个山坡,如果沿山坡在水平AC方向上每前进100m铅直高度就升高60m,那么用科学计算器求坡角∠A的度数,并以“度、分、秒”为单位表示出这个度数,下列按键顺序正确的是( )| A. |  | |
| B. |  | |
| C. |  | |
| D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
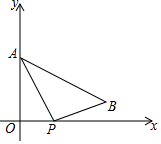 如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:
如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
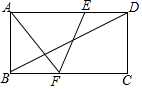 如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.
如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com