
【题目】如图A,B,D在同一条直线上,∠A=∠D=90°,AB=DE,∠BCE=∠BEC,
(1)求证:△ACB≌△DBE
(2)求证:CB⊥BE

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等角对等边可得:BC=EB,再利用HL即可证出Rt△ACB≌Rt△DBE;
(2)由Rt△ACB≌Rt△DBE,可得:∠ABC=∠DEB,再根据∠DEB+∠DBE=90°,从而得出:∠ABC+∠DBE=90°,即可得出∠CBE=90°,即CB⊥BE.
证明:(1)∵∠BCE=∠BEC
∴BC=EB
在Rt△ACB和Rt△DBE中
![]()
∴Rt△ACB≌Rt△DBE
(2)∵Rt△ACB≌Rt△DBE
∴∠ABC=∠DEB
∵∠D=90°
∴∠DEB+∠DBE=90°
∴∠ABC+∠DBE=90°
∴∠CBE=180°-(∠ABC+∠DBE)=90°
∴CB⊥BE


科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10……) 和“正方形数”(如1,4,9,16……),在小于200的数中,设最大的“三角形数”为t,最大的“正方形数”为m,则t+m的值为( )

A.33B.301C.386D.571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,过点
中点,过点![]() 的直线分别与
的直线分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,则下列结论:
,则下列结论:
①![]() ,
,![]() ;
;
②![]() ;
;
③四边形![]() 是菱形;
是菱形;
④![]() .
.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形△ABC边长为a,等腰三角形△BDC中,∠BDC=120,∠MDN=60,角的两边分别交AB,AC于点M,N,连结MN.则△AMN的周长为( )
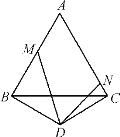
A.aB.2aC.3aD.4a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
爱动脑筋的小明发现二次三项式也可以配方,从而解决一些问题.
例如:x2﹣6x+10=(x2﹣6x+9)+1=(x﹣3)2+1≥0;因此x2﹣6x+10有最小值是1.
(1)尝试:﹣3x2﹣6x+5=﹣3(x2+2x+1﹣1)+5=﹣3(x+1)2+8,因此﹣3x2﹣6x+5有最大值是 .
(2)应用:有长为28米的篱笆,一面利用墙(墙的最大可用长度为16米),围成一个长方形的花圃.能围成面积最大的花圃吗?如果能,请求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com