

分析 (1)先用非负性求出a,b,从而确定出直线BC的解析式,进而求出直线AH解析式,即可;
(2)先求出OG解析式,进而求出G坐标,即可求出OG和OH,用三角函数即可;
(3)先求出点E坐标,从而确定出直线BE解析式,设出点N坐标,用角平分线的性质即可求出m即可.
解答 解:(1)∵(a+b)2+(a-4)2=0.
∴a=4,b=-4,
∴A(4,0),B(0,-4),
∵C的坐标为(-1,0),
∴直线BC解析式为y=-4x-4,
∵AH⊥BC,
设直线AH解析式为y=$\frac{1}{4}$x+b,
∵A(4,0)在直线AH上,
∴1+b=0,
∴b=-1,
∴直线AH解析式为y=$\frac{1}{4}$x-1,
∴P(0,-1);
(2)如图2,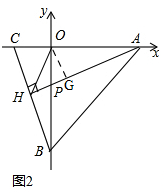
由(1)知,直线BC解析式为y=-4x-4①,
直线AH解析式为y=$\frac{1}{4}$x-1②,
联立①②得H(-$\frac{12}{17}$,-$\frac{20}{17}$)
∴OH2=(-$\frac{12}{17}$)2+(-$\frac{20}{17}$)2=$\frac{544}{1{7}^{2}}$,
过点O作OG⊥AH,
∴OG∥BC,
∴直线OG解析式为y=-4x③,
由②③得,G($\frac{4}{17}$,-$\frac{16}{17}$),
∴OG2=($\frac{4}{17}$)2+(-$\frac{16}{17}$)2=$\frac{272}{1{7}^{2}}$,
∴$\frac{O{G}^{2}}{O{H}^{2}}=\frac{1}{2}$,
∴$\frac{OG}{OH}$=$\frac{\sqrt{2}}{2}$,
∴sin∠AHO=$\frac{OG}{OH}=\frac{\sqrt{2}}{2}$,=
∴∠AHO=45°,
(3)如图,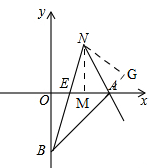
∵S△OEB:S△EAB=1:$\sqrt{2}$,
∴$\frac{OE}{AE}=\frac{1}{\sqrt{2}}$,
由(1)知,OA=4,
∴OE=4($\sqrt{2}-1$),
∴E(4($\sqrt{2}$-1),0),
∴直线BE解析式为y=($\sqrt{2}$+1)x-4,
设点N(m,($\sqrt{2}$+1)m-4),(m>0)
∴MN=($\sqrt{2}$+1)m-4
∵A(4,0),B(0,-4),
∴直线AB解析式为y=x-4,
∴NG=$\frac{|m-(\sqrt{2}+1)m+4-4|}{\sqrt{2}}$=|m|=m,
∵点N在角平分线上,
∴MN=NG.
∴($\sqrt{2}$+1)m-4=m,
∴m=2$\sqrt{2}$,
∴N(2$\sqrt{2}$,2$\sqrt{2}$).
点评 此题三角形综合题,主要考查了非负性,待定系数法,直线的交点坐标,三角函数,角平分线的性质,解本题的关键是用三角函数求出∠AHO,难点是求出点N的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,等腰△ABC中,AB=AC,∠A=120,BC=6cm,线段AB垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于点N,交AC于点F,则MN=2cm.
如图,等腰△ABC中,AB=AC,∠A=120,BC=6cm,线段AB垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于点N,交AC于点F,则MN=2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 5 | x | y | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.若△BED的面积为28,△DFC的面积为21,求△DEF的面积.
如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.若△BED的面积为28,△DFC的面积为21,求△DEF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在2×4的正方形方格中,有格点△ABC(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与△ABC相似但不全等的格点三角形共有( )
如图,在2×4的正方形方格中,有格点△ABC(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与△ABC相似但不全等的格点三角形共有( )| A. | 4个 | B. | 8个 | C. | 16个 | D. | 20个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com