
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C、D不重合).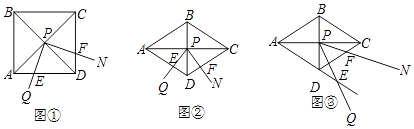
(1)如图①,当α=90°时,求证:DE+DF=AD.
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为 ![]() ,请给出证明.
,请给出证明.
(3)在(2)的条件下,将∠QPN绕点P旋转,若旋转过程中∠QPN的边PQ与边AD的延长线交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
【答案】
(1)
证明:正方形ABCD的对角线AC,BD交于点P,
∴PA=PD,∠PAE=∠PDF=45°,
∵∠APE+∠EPD=∠DPF+∠EPD=90°,
∴∠APE=∠DPF,
在△APE和△DPF中
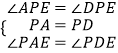 ,
,
∴△APE≌△DPF(ASA),
∴AE=DF,
∴DE+DF=AD
(2)
如图②,取AD的中点M,连接PM,
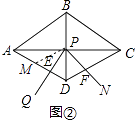
∵四边形ABCD为∠ADC=120°的菱形,
∴BD=AD,∠DAP=30°,∠ADP=∠CDP=60°,
∴△MDP是等边三角形,
∴PM=PD,∠PME=∠PDF=60°,
∵∠PAM=30°,
∴∠MPD=60°,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,
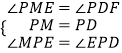 ,
,
∴△MPE≌△DPF(ASA)
∴ME=DF,
∴DE+DF= ![]() AD
AD
(3)
如图,
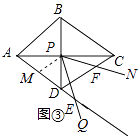
如图③,当点E落在AD的延长线上时,
取AD的中点M,连接PM,
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,
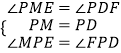 ,
,
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DF﹣DE=ME﹣DE=DM= ![]() AD
AD
【解析】(1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME= ![]() AD,即可得出DE+DF=
AD,即可得出DE+DF= ![]() AD,(3)①当点E落在AD上时,DE+DF=
AD,(3)①当点E落在AD上时,DE+DF= ![]() AD,②当点E落在AD的延长线上时,DF﹣DE=
AD,②当点E落在AD的延长线上时,DF﹣DE= ![]() AD.
AD.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE. 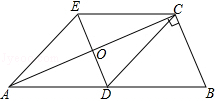
(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是一个平行四边形,BE⊥CD于点E,BF⊥AD于点F, 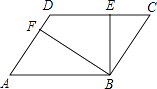
(1)请用图中表示的字母表示出平行线AD与BC之间的距离;
(2)若BE=2cm,BF=4cm,求平行线AB与CD之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组7位同学的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是( )
A. 30,27 B. 30,29 C. 29,30 D. 30,28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:如图,正方形ABCD中,E、F分别为AB、AD上的点,AF=BE,CE、BF交于H,BF交AC于M,O为AC的中点,OB交CE于N,连OH.下列结论中:①BF⊥CE;②OM=ON;③ ![]() ;④
;④ ![]() .其中正确的命题有( )
.其中正确的命题有( ) 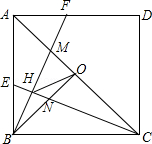
A.只有①②
B.只有①②④
C.只有①④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB= ![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG. 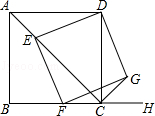
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com