

 =
=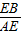 ,
,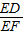 =
=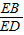


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
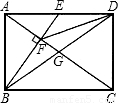
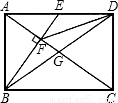
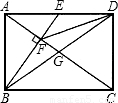
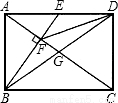
 17、(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )
17、(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )查看答案和解析>>
科目:初中数学 来源:第19章《相似形》中考题集(05):19.5 相似三角形的判定(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:第29章《相似形》中考题集(05):29.4 三角形相似的条件(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2012年安徽省滁州市凤阳县城西中学中考数学模拟试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com