
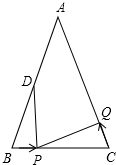
 如图,已知△ABC中,AB=AC=8cm,∠B=∠C,BC=5cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=8cm,∠B=∠C,BC=5cm,点D为AB的中点.分析 (1)①根据等腰三角形的性质,得到∠B=∠C,再结合BP=CQ=1,PC=BD=4,则可利用SAS判定△BPD与△CQP全等;
②设当点Q的运动速度为a厘米/秒,时间是t秒时,能够使△BPD与△CQP全等,根据点Q的运动速度与点P的运动速度不相等,可得BP和CQ不是对应边,根据BD=CQ,BP=CP,可得t和a的值;
(2)求出Q的运动路程,与根据三角形ABC周长的整数倍进行比较,即可得出相遇点的位置.
解答  解:(1)①△BPD≌△CQP.
解:(1)①△BPD≌△CQP.
理由如下:
∵t=1s,
∴BP=CQ=1×1=1(cm),
∵AB=8cm,点D为AB的中点,
∴BD=4cm,
又∵PC=BC-BP,BC=5cm,
∴PC=5-1=4(cm),
∴PC=BD,
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
$\left\{\begin{array}{l}{BP=CQ}\\{∠B=∠C}\\{BD=CP}\end{array}\right.$,
∴△BPD≌△CQP(SAS),
即经过1秒后,△BPD与△CQP全等;
②设当点Q的运动速度为a厘米/秒,时间是t秒时,能够使△BPD与△CQP全等,
∵点Q的运动速度与点P的运动速度不相等,
∴BP和CQ不是对应边,
即BD=CQ,BP=CP,
即t=5-t,
解得:t=2.5,
∵BD=CQ,
∴4=2.5a,
解得:a=1.6;
即当点Q的运动速度为1.6cm/s,运动时间为$\frac{5}{2}$秒时,能够使△BPD与△CQP全等;
(2)设经过t秒时,P、Q第一次相遇,
∵P的速度是1厘米/秒,Q的速度是1.6厘米/秒,
∴8+8+1t=1.6t,
解得:t=$\frac{80}{3}$,
此时点Q的路程=1.6×$\frac{80}{3}$=$\frac{128}{3}$(厘米),
∵$\frac{128}{3}$÷(8+8+5)=2$\frac{2}{63}$,$\frac{2}{63}$×(8+8+5)=$\frac{2}{3}$<8,
∴经过$\frac{80}{3}$秒后点P与点Q第一次在△ABC的边AC上相遇.
故答案为:$\frac{80}{3}$,AC.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,等腰三角形的性质以及数形结合思想的运用,解题的关键是熟练掌握三角形全等的判定和性质.解题时注意全等三角形的对应边相等.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
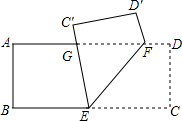 如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,若∠EFG=60°,试求∠BEG的度数.
如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,若∠EFG=60°,试求∠BEG的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化/万人 | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | -0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:在数轴上点A表示数a,点B表示数b,点C表示数c,b是最大的负整数,且a、c满足|a+3|+(c-5)2=0.
如图:在数轴上点A表示数a,点B表示数b,点C表示数c,b是最大的负整数,且a、c满足|a+3|+(c-5)2=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com