
分析 设f(x)=3x2-5x+m,由题意可得$\left\{\begin{array}{l}{{f}_{(-2)}=22+m>0}\\{{f}_{(1)}=-2+m<0}\\{{f}_{(3)}=12+m>0}\end{array}\right.$,可得m的取值范围.
解答 解:设f(x)=3x2-5x+m,
由题意可得$\left\{\begin{array}{l}{{f}_{(-2)}=22+m>0}\\{{f}_{(1)}=-2+m<0}\\{{f}_{(3)}=12+m>0}\end{array}\right.$,
解得:-12<m<2,
故答案为:-12<m<2.
点评 本题主要考查了抛物线与x轴的交点,利用函数思想是解答此题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
 如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色)小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.
如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色)小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ③⑤ | C. | ②④⑤ | D. | ③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
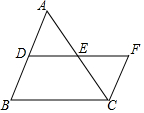 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )| A. | 1:3 | B. | 2:3 | C. | 2:5 | D. | 1:4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com