
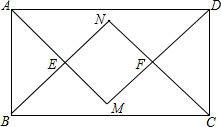
 矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形.
矩形ABCD四个内角平分线组成四边形MFNE,求证:四边形MFNE是正方形. 分析 首先根据已知条件证明四边形EMFN是矩形,再根据正方形的判定:邻边相等的矩形是正方形即证明FM=EM即可
解答 证明:∵四边形ABCD是矩形,
∴四个内角均为90°,
∵AE,BE,CF,DF分别是四个内角的平分线,
∴∠NBC=∠NCB=45°,
∴△NBC为等腰直角三角形,
∴∠N=90°,
同理∠M=∠NEM=∠NFM=90°,
∴四边形MFNE为矩形,
∵AD=BC,∠M=∠N=90°,∠DAM=∠NBC=45°,
∴△DAM≌△CBN(AAS)
∴AM=BN,
∵AE=BE,
∴AM-AE=BN-BF,即FM=EM,
∴四边形MFNE是正方形.
点评 本题考查了矩形的性质和判定、角平分线的性质等腰直角三角形的判定和性质以及正方形的判定,解题的关键是对特殊的几何图形的判定和性质要熟练掌握.


科目:初中数学 来源: 题型:填空题
 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
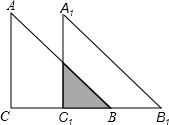 如图所示,已知ABC,∠C=90°,AC=BC=4,现将△ABC沿CB方向平移到△A1B1C1的位置.
如图所示,已知ABC,∠C=90°,AC=BC=4,现将△ABC沿CB方向平移到△A1B1C1的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2是不等式3x>5的一个解 | B. | x=2是不等式3x>5的解 | ||
| C. | x=2是不等式3x>5的唯一解 | D. | x=2不是不等式3x>5的解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com