
 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )| A. | 72° | B. | 54° | C. | 36° | D. | 30° |
分析 由折叠易得∠EDC′=∠EDC,根据平行及等腰梯形的性质可得DE=DC,那么∠C=∠DEC=∠B=72°,根据三角形内角和定理可得∠EDC的度数,也就求得了∠EDC′的度数.
解答 解:∵平行移动腰AB至DE,
∴DE=AB=CD,
∴∠C=∠DEC=∠B=72°,∠EDC=180°-2∠C=36°,
由折叠的性质知,∠EC′D=∠C=72°,
∴∠EDC'=180°-2∠EC′D=36°,
故选:C.
点评 本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、等腰梯形的性质,等边对等角,三角形的内角和定理等知识点.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表| 岗位 | 经理 | 技师 | 领班 | 助理 | 服务员 | 清洁工 |
| 基本工资 | 10000 | 4000 | 2400 | 1600 | 1000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
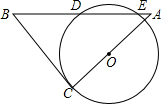 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一天,小青在校园内发现一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.5米,由此可推断出树高是3米.
一天,小青在校园内发现一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.5米,由此可推断出树高是3米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠,点B落在点E处交DC于点F,则△ADF和△EFC的周长之和为14cm.
如图,四边形ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠,点B落在点E处交DC于点F,则△ADF和△EFC的周长之和为14cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com