
【题目】如图,已知一次函数y=﹣ ![]() x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA. 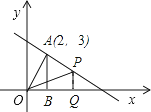
(1)求此一次函数的解析式;
(2)设点P为直线y=﹣ ![]() x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ=
x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
【答案】
(1)
解:∵一次函数y=﹣ ![]() x+b的图象经过点A(2,3),
x+b的图象经过点A(2,3),
∴3=(﹣ ![]() )×2+b,
)×2+b,
解得b=4,
故此一次函数的解析式为:y=﹣ ![]() x+4
x+4
(2)
解:设P(p,d),p>0,
∵点P在直线y=﹣ ![]() x+4的图象上,
x+4的图象上,
∴d=﹣ ![]() p+4①,
p+4①,
∵S△POQ= ![]() S△AOB=
S△AOB= ![]() ×
× ![]() ×2×3,
×2×3,
∴ ![]() pd=
pd= ![]() ②,
②,
①②联立得, 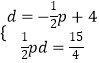 ,
,
解得 ![]() 或
或 ![]() ,
,
∴P点坐标为:(3, ![]() )或(5,
)或(5, ![]() )
)
【解析】(1)直接把点A(2,3)代入一次函数y=﹣ ![]() x+b即可求出b的值,进而得出一次函数的解析式;(2)设P(p,d),p>0,再根据点P在一次函数的图象上及S△POQ=
x+b即可求出b的值,进而得出一次函数的解析式;(2)设P(p,d),p>0,再根据点P在一次函数的图象上及S△POQ= ![]() S△AOB , 即可得出关于p、d的方程组,求出p、d的值即可.
S△AOB , 即可得出关于p、d的方程组,求出p、d的值即可.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由; 
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l∥AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )

A. ①②④ B. ①③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.

(1)求证:△OAE≌△OCF;
(2)若OA=OD,猜想:四边形ABCD的形状,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体水果店经营某种水果,进价![]() 元/千克,售价
元/千克,售价![]() 元/千克,
元/千克,![]() 月
月![]() 日至
日至![]() 月
月![]() 日经营情况如下表:
日经营情况如下表:
日期 |
|
|
|
|
|
购进 |
|
|
|
|
|
售出 |
|
|
|
|
|
损耗 |
|
|
|
|
|
![]() 若
若![]() 月
月![]() 日的库存为
日的库存为![]() ,则
,则![]() 月
月![]() 日的库存为________;
日的库存为________;
![]() 就
就![]() 月
月![]() 日经营情况看,当天是赚还是赔了?
日经营情况看,当天是赚还是赔了?
![]() 每天交卫生费
每天交卫生费![]() 元,则
元,则![]() 月
月![]() 日
日![]() 月
月![]() 日该个体户共赚多少钱?
日该个体户共赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
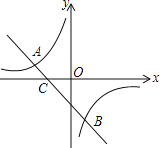
【题目】如图,已知A(﹣3,1),B(1, ![]() )是一次函数
)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出使一次函数的函数值小于反比例函数的函数值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com