
如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.
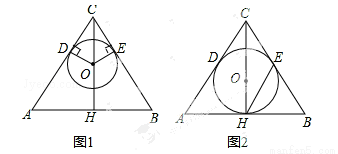
(1)求证:⊙O与CB相切于点E;
(2)如图2,若⊙O过点H,且AC=5,AB=6,连接EH,求△BHE的面积.
(1)证明见解析;(2)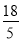 .
.
【解析】
试题分析:(1)由CA=CB,且CH垂直于AB,利用三线合一得到CH为角平分线,再由OD垂直于AC,OE垂直于CB,利用角平分线定理得到OE=OD,利用切线的判定方法即可得证;
(2)由CA=CB,CH为高,利用三线合一得到AH=BH,在直角三角形ACH中,利用勾股定理求出CH的长,由圆O过H,CH垂直于AB,得到圆O与AB相切,由(1)得到圆O与CB相切,利用切线长定理得到BE=BH,如图所示,过E作EF垂直于AB,得到EF与CH平行,得出△BEF与△BCH相似,由相似得比例,求出EF的长,由BH与EF的长,利用三角形面积公式即可求出△BEH的面积.
试题解析:(1)证明:∵CA=CB,点O在高CH上,
∴∠ACH=∠BCH,
∵OD⊥CA,OE⊥CB,
∴OE=OD,
∴圆O与CB相切于点E;
(2)【解析】
∵CA=CB,CH是高,
∴AH=BH=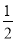 AB=3,
AB=3,
∴CH=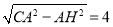 ,
,
∵点O在高CH上,圆O过点H,
∴圆O与AB相切于H点,
由(1)得圆O与CB相切于点E,
∴BE=BH=3,
如图,过E作EF⊥AB,则EF∥CH,

∴△BEF∽△BCH,
∴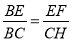 ,
,
即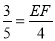 ,
,
解得:EF=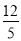 ,
,
∴S△BHE=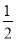 BH•EF=
BH•EF=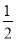 ×3×
×3×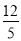 =
=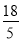 .
.
考点:1.切线的判定与性质;2.勾股定理;3.相似三角形的判定与性质.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:2014-2015学年湖南省株洲市攸县七年级上学期期末测试数学试卷(解析版) 题型:解答题
(本题满分6分,每小题3分)
(1)计算: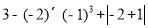
(2)已知A=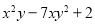 ,B=
,B=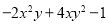 ,求2A+B.
,求2A+B.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如果点A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数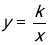 (k>0)的图象上,那么,y1,y2,y3的大小关系是( )
(k>0)的图象上,那么,y1,y2,y3的大小关系是( )
A.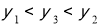 B.
B.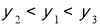
C.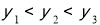 D.
D.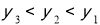
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
一元二次方程x2+px-6=0的一个根为2,则p的值为( )
A.-1 B.-2 C.1 D.2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:解答题
为了倡导“节约用水,从我做起”,宜兴市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
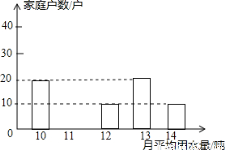
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计宜兴市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:解答题
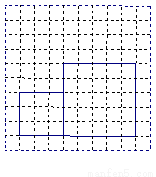
已知两个连体的正方形(有两条边在同一条直线上)在正方形网格上的位置如图所示,请你把它分割后,拼接成一个新的正方形. (要求:在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上,不写作法).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:填空题
抛物线y=2x2向左平移1个单位,再向下平移3个单位,得到的抛物线表达式为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com