
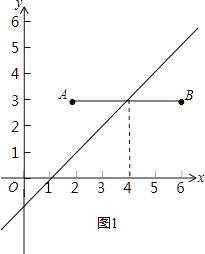
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A(2��3)��B(6��3)������AB��������ƽ����һ��P���߶�AB�϶����ڵ�Q��ʹ��PQ��1����Ƶ�P���߶�AB���ڽ��㣮
��1���жϵ�D(![]() ��
��![]() )�Ƿ����߶�AB���ڽ��㣮________�����ǻ��
)�Ƿ����߶�AB���ڽ��㣮________�����ǻ��
��2������H(m��n)��һ�κ���y��x��1��ͼ���ϣ������߶�AB���ڽ��㣬��m��ȡֵ��Χ��
��3����һ�κ���y��x��b��ͼ�������ٴ���һ���ڽ��㣬ֱ��д��b��ȡֵ��Χ��

���𰸡���1���ǣ���2��3��m��5����3����![]() ��3��b��
��3��b��![]() +1
+1
��������
��1������A��B������ó�AB��x�ᣬ���ݵ�P��ֱ��AB�ľ�����1�������������2��x��6������2��y��4��Χ��ʱ�������߶�AB�����ٽ�������������������Ƿ���y�ķ�Χ�ڼ����Լ���A�����ߵ�A��ľ�����1������B����ұߵ�B��ľ�����1�������߶�AB�ġ��ٽ��㡱��
��2�������ֱ��y��x��1���߶�AB���ڣ�4��3����Ȼ�������������ۣ��ٵ�m��4ʱ�������߶�AB�����ٽ�������������ķ�Χ��2��n��4����n��2��n��4�ֱ����n��m��1�������Ӧ��mֵ�����ɵó���ĺ�����m�ķ�Χ��
��3����ͼ���ֱ����N1��N2�����꣬Ȼ����ݴ���ϵ�����ֱ���ú�����Ϊ2��������Ϊ3+![]() �������Ϊ6��������Ϊ3��
�������Ϊ6��������Ϊ3��![]() ʱ��ֱ��y��x+b��bֵ�����˿���b��ȡֵ��Χ��
ʱ��ֱ��y��x+b��bֵ�����˿���b��ȡֵ��Χ��
��1����D���߶�AB�ġ��ڽ��㡱��
��AD�� ��1��
��1��
��D��![]() ��
��![]() �����߶�AB�����ٽ�������
�����߶�AB�����ٽ�������
��2����ͼ1���ߵ�H��m��n�����߶�AB�����ڽ���������H��m��n����ֱ��y��x��1�ϣ�
��n��m��1��
ֱ��y��x��1���߶�AB���ڣ�4��3��
�ٵ�m��4ʱ����n��m��1��3��
��AB��x�ᣬ
���ʱ��H��m��n�����߶�AB�ľ�����n��3��
��0��n��3��1��
��4��m��5��
�ڵ�m��4ʱ����n��m��1��
��n��3��
��AB��x�ᣬ
���ʱ��H��m��n�����߶�AB�ľ�����3��n��
��0��3��n��1��
��3��m��4��
����������3��m��5��
��3������ͼ2��
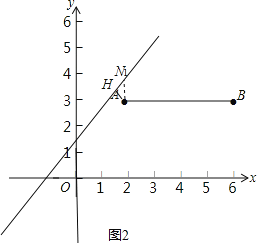
��ֱ��y��x+b��֪��AN1H��45����
��AH��1��
��AN1��![]() ��
��
��N1��2��3+![]() ����
����
�Ѻ�����2��������3+![]() ����ֱ��y��x+b���ɵ�3+
����ֱ��y��x+b���ɵ�3+![]() ��2+b�����b��
��2+b�����b��![]() +1��
+1��
����ͼ3��
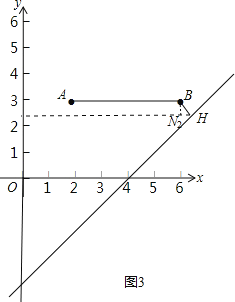
ͬ��֤��N2��6��3��![]() ����
����
�Ѻ�����6��������3��![]() ����ֱ��y��x+b���ɵ�3��
����ֱ��y��x+b���ɵ�3��![]() ��6+b�����b����
��6+b�����b����![]() ��3��
��3��
��b��ȡֵ��ΧΪ��![]() ��3��b��
��3��b��![]() +1��
+1��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��Ӯ��40Ԫ��Ϊ���������ۣ�����Ӯ����������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2������
��1�����̳�ƽ��ÿ��ҪӮ��1200Ԫ��ÿ������Ӧ���۶���Ԫ��
��2��ÿ���������۶���Ԫʱ���̳�ƽ��ÿ��Ӯ����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��![]() �Ķ�����ڸ���ϣ���
�Ķ�����ڸ���ϣ���![]() ������Ϊ
������Ϊ![]() ��
��

����![]() ����ƽ��5����λ��õ���Ӧ��
����ƽ��5����λ��õ���Ӧ��![]() ������
������![]() �����
����д��![]() �����ꣻ
�����ꣻ
����ԭ��![]() Ϊ�Գ����ģ�����
Ϊ�Գ����ģ�����![]() �����ԭ��
�����ԭ��![]() �ԳƵ�
�ԳƵ�![]() ����д����
����д����![]() �����꣮
�����꣮
����ԭ��OΪ��ת���ģ�������![]() ˳ʱ����ת90����ͼ����A3B3C3����д��C3�����꣮
˳ʱ����ת90����ͼ����A3B3C3����д��C3�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж���ȷ���ǣ� ����
A.����3��5��4��1��-2����λ��Ϊ4
B.�ӳ����¿��ɼ��г�ȡ100��ѧ������ѧ�ɼ�����100��ѧ���������һ������
C.�ס������˸����5�Σ���֪����![]() ��
��![]() ����ô�ҵ�����ɼ����ȶ�
����ô�ҵ�����ɼ����ȶ�
D.�˽�����ʡ�����о��������ڼ�ij��з�ʽ������ȫ�����ķ�ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
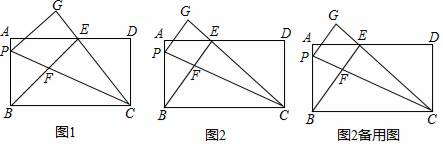
����Ŀ���ھ���ABCD�У�AB=12��P�DZ�AB��һ�㣬����PBC��ֱ��PC�۵�������B�Ķ�Ӧ���ǵ�G������B��BE��CG������ΪE����AD�ϣ�BE��PC�ڵ�F��
��1����ͼ1������E��AD���е㣬��֤����AEB�ա�DEC��
��2����ͼ2������֤��BP=BF��
�ڵ�AD=25����AE��DEʱ����cos��PCB��ֵ��
�۵�BP=9ʱ����BEEF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
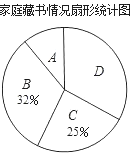
����Ŀ����������У����У�ijУΪ�˽�ѧ����ͥ��������������ȡ��У����ѧ�����е��飬�����Ƴɲ���ͳ��ͼ�����£�
��� | ��ͥ����m�� | ѧ������ |
A | 0��m��25 | 20 |
B | 26��m��100 | a |
C | 101��m��200 | 50 |
D | m��201 | 66 |
����������Ϣ������������⣺
(1)�õ������������Ϊ_____��a��_____��
(2)������ͳ��ͼ�У���A����Ӧ���ε�Բ�Ľ�Ϊ_____����
(3)����У��2000��ѧ���������ȫУѧ���м�ͥ����200�����ϵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y����x2+bx+c������A��2��0����B��0��2����
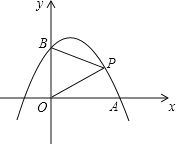
��1�������������ߵĽ���ʽ��
��2����ͼ����P����������һ���㣬����BP��OP������BOP����BOΪ�ױߵĵ��������Σ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() ��
��![]() ����һ��
����һ��![]() ������
������![]() ��
��![]() ��
��
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��ֱ��
��ֱ��![]() �Ϸ���Բ����һ���㣬
�Ϸ���Բ����һ���㣬![]() �İ뾶Ϊ2����
�İ뾶Ϊ2����
�ٵ���![]() �ij��� ʱ����
�ij��� ʱ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����������Σ�
Ϊ������ı����������Σ�
�ڵ�![]() �ij����� ʱ����
�ij����� ʱ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı��������Σ�
Ϊ������ı��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
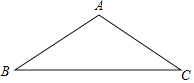
����Ŀ����ͼ����ABC��
��1���߹���ͼ��
�������ױߵ�����AD��
����AB��ȡ��E��ʹBE��BD��
��2���ڣ�1���Ļ����ϣ���AB��AC����BAC��120�㣬���ADE�Ķ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com