
如图,直线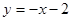 交x轴于点A,交y轴于点B,抛物线
交x轴于点A,交y轴于点B,抛物线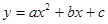 的顶点为A,且经过点B.
的顶点为A,且经过点B.
⑴求该抛物线的解析式;
⑵若点C(m, )在抛物线上,求m的值.
)在抛物线上,求m的值.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
 已知:抛物线
已知:抛物线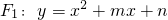 的顶点为A(1,0)
的顶点为A(1,0)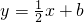 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线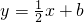 对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式;
对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式; ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
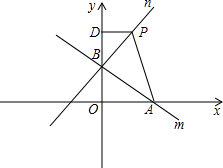 如图,直线
如图,直线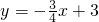 交x轴于点A,交y轴于点B,第一象限内的点P(a,b)是经过点B的直线n上的一点,过点P作PD⊥y轴于点D,连结PA.
交x轴于点A,交y轴于点B,第一象限内的点P(a,b)是经过点B的直线n上的一点,过点P作PD⊥y轴于点D,连结PA.查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省恩施州利川市东城初中九年级(上)入学选拔考试数学试卷(解析版) 题型:解答题
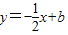 交x轴于点A,交直线
交x轴于点A,交直线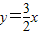 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.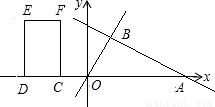
查看答案和解析>>
科目:初中数学 来源:2008年吉林省长春市中考数学模拟试卷(解析版) 题型:解答题
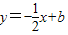 交x轴于点A,交直线
交x轴于点A,交直线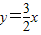 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.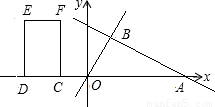
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省南通市通州区九年级中考适应性考试(一模)数学试卷(解析版) 题型:解答题
已知:如图,直线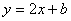 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.

(1)求b的值;
(2)若点P是线段AB中垂线上的点,是否存在这样的点P,使△PBC成为直角三角形.若存在,试直接写出所有符合条件的点P的坐标;若不存在,试说明理由;
(3)点Q为线段AB上一个动点(点Q与点A、B不重合),QE∥AC,交BC于点E,以QE为边,在点B的异侧作正方形QEFG.设AQ=m,△ABC与正方形QEFG的重叠部分的面积为S,试求S与m之间的函数关系式,并写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com