
【题目】本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定,顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
(1)顾客小华消费150元,获得打折待遇的概率是多少?
(2)顾客小明消费120元,获得五折待遇的概率是多少?
(3)小华对小明说:“我们用这个转盘来做一个游戏,指针指到五折你赢,指针指到七折算我赢”,你认为这个游戏规则公平吗?请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)公平,理由见解析.
;(3)公平,理由见解析.
【解析】
(1)由顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,即可得顾客小华消费150元,能获得1次转动转盘的机会;由共有8种等可能的结果,有5次打折机会,直接利用概率公式求解即可求得答案
(2)利用获得打五折待遇的有2种情况,直接利用概率公式求解即可求得答案;
(3)由共有8种等可能的结果,获得七折待遇的有2种情况,直接利用概率公式求解即可求得答案,进而比较得出答案.
解:(1)∵顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,
∴顾客小华消费150元,能获得1次转动转盘的机会,
∵共有8种等可能的结果,获得打折待遇的有5种情况,
∴小华获得打折待遇的概率是:![]() ;
;
(2)∵共有8种等可能的结果,获得五折待遇的有2种情况,
∴获得五折待遇的概率是:![]() ;
;
(3)公平,
∵共有8种等可能的结果,获得七折待遇的有2种情况,
∴获得七折待遇的概率是:![]() ;
;
则两人获胜的概率相同都为:![]() ,故此游戏公平.
,故此游戏公平.
故答案为:(1)![]() ;(2)
;(2)![]() ;(3)公平,理由见解析.
;(3)公平,理由见解析.


科目:初中数学 来源: 题型:
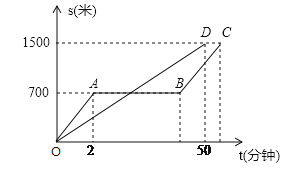
【题目】“龟免赛跑”的故事同学们都非常热悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中_______(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是___________米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来假,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线。
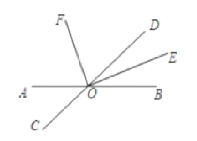
(1)∠DOE的补角是___;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
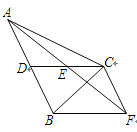
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系:

(1)在这个变化过程中自变量是_________,因变量是___________;
(2)小李_________时到达离家最远的地方,此时离家_________km;
(3)分别求出在1≤t≤2时和2≤t≤4时小李骑自行车的速度;
(4)请直接写出小李何时与家相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
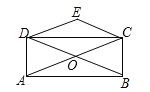
A.4B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com