
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
【答案】
(1)解:把点B的坐标为(3,0)代入抛物线y=﹣x2+mx+3得:0=﹣32+3m+3,
解得:m=2,
∴y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为:(1,4)
(2)解:连接BC交抛物线对称轴l于点P,
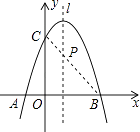
则此时PA+PC的值最小,
设直线BC的解析式为:y=kx+b,
∵点C(0,3),点B(3,0),
∴ ![]() ,
,
解得: ![]() ,
,
∴直线BC的解析式为:y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴当PA+PC的值最小时,点P的坐标为:(1,2).
【解析】(1)首先把点B的坐标为(3,0)代入抛物线y=﹣x2+mx+3,利用待定系数法即可求得m的值,继而求得抛物线的顶点坐标;(2)首先连接BC交抛物线对称轴l于点P,则此时PA+PC的值最小,然后利用待定系数法求得直线BC的解析式,继而求得答案.


科目:初中数学 来源: 题型:
【题目】画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.

(1)将△ABC向左平移8格,再向下平移1格.请在图中画出平移后的△A′B′C′
(2)利用网格在图中画出△ABC的中线CD,高线AE;
(3)△A′B′C′的面积为_____.
(4)在平移过程中线段BC所扫过的面积为 .
(5)在右图中能使![]() 的格点P的个数有 个(点P异于A).
的格点P的个数有 个(点P异于A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
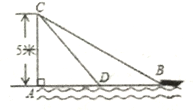
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2 , 当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=6,BC=8,tan∠B= ![]() ,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() ABC的三个顶点坐标分别为A(3,5),B(4,3),
ABC的三个顶点坐标分别为A(3,5),B(4,3),
C(1,1).
(1)画出![]() ABC关于x轴对称的
ABC关于x轴对称的![]() A1B1C1;并填写出
A1B1C1;并填写出![]() A1B1C三个顶点的坐标.
A1B1C三个顶点的坐标.
A1 (_________,_________);
B1 (_________,________);
C1 (_________,_________).
(2)求![]() ABC的面积.
ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正确的结论有_______________(填结论前面的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com