
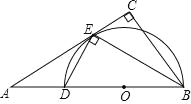
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=2![]() ,AE=6,求EC的长.
,AE=6,求EC的长.
【答案】(1)证明见解析(2)3
【解析】
试题分析:(1)取BD的中点0,连结OE,如图,由∠BED=90°,根据圆周角定理可得BD为△BDE的外接圆的直径,点O为△BDE的外接圆的圆心,再证明OE∥BC,得到∠AEO=∠C=90°,于是可根据切线的判定定理判断AC是△BDE的外接圆的切线;
(2)设⊙O的半径为r,根据勾股定理得62+r2=(r+2![]() )2,解得r=2
)2,解得r=2![]() ,根据平行线分线段成比例定理,由OE∥BC得
,根据平行线分线段成比例定理,由OE∥BC得![]() ,然后根据比例性质可计算出EC.
,然后根据比例性质可计算出EC.
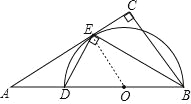
试题解析:(1)证明:取BD的中点0,连结OE,如图,
∵DE⊥EB,
∴∠BED=90°,
∴BD为△BDE的外接圆的直径,点O为△BDE的外接圆的圆心,
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠EB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴OE⊥AE,
∴AC是△BDE的外接圆的切线;
(2)解:设⊙O的半径为r,则OA=OD+DA=r+2![]() ,OE=r,
,OE=r,
在Rt△AEO中,∵AE2+OE2=AO2,
∴62+r2=(r+2![]() )2,解得r=2
)2,解得r=2![]() ,
,
∵OE∥BC,
∴![]() ,即
,即![]() ,
,
∴CE=3.


科目:初中数学 来源: 题型:
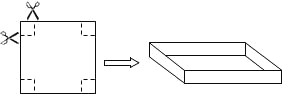
【题目】把一张边长为40cm的正方形硬纸板进行裁剪,折成一个长方体盒子(纸板的厚度忽略不计).如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
(1)若剪掉的正方形的边长为9cm时,长方体盒子的底面边长为 cm,高为 cm.
(2)要使折成的长方体盒子的底面积为484cm2,那么剪掉的正方形边长为多少?
(3)折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
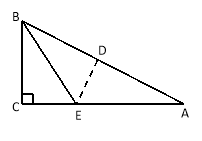
【题目】在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,如图,使点A和点B重合,折痕与AB、AC分别相交于点D和点E,折痕DE的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
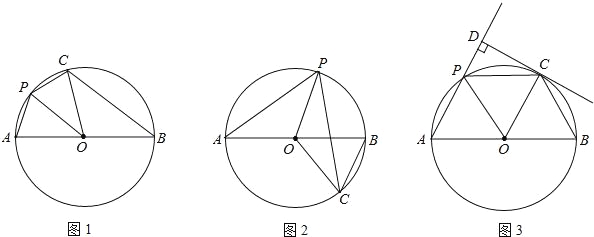
【题目】已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:
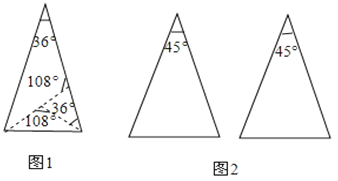
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)![]() 中,∠B=30°,AD和DE是
中,∠B=30°,AD和DE是![]() 的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用量角器度量几个角的度数,下列结论中正确的是( )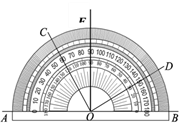
A.∠BOC=60°
B.∠COA是∠EOD 的余角
C.∠AOC=∠BOD
D.∠AOD与∠COE互补
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com