
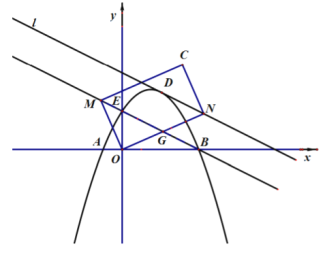
【题目】已知:如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 点和
点和![]() 点(
点(![]() 点在
点在![]() 点左则),交
点左则),交![]() 轴于
轴于![]() 点,作直线
点,作直线![]() 是直线
是直线![]() 上方抛物线上的一个动点.过
上方抛物线上的一个动点.过![]() 点作 直线
点作 直线![]() 平行于直线
平行于直线![]() 是直线
是直线 ![]() 上的任意点,
上的任意点,![]() 是直线
是直线![]() 上的任意点,连接
上的任意点,连接![]() ,始终保持
,始终保持![]() 为
为![]() ,以
,以![]() 和
和![]() 边,作矩形
边,作矩形![]() .
.
(1)在![]() 点移动过程中,求出当
点移动过程中,求出当![]() 的面积最大时点
的面积最大时点![]() 的坐标;在
的坐标;在![]() 的面积最大 时,求矩形
的面积最大 时,求矩形![]() 的面积的最小值.
的面积的最小值.
(2)在![]() 的面积最大时,线段
的面积最大时,线段![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 四个点组成平行 四边形时,求此时线段
四个点组成平行 四边形时,求此时线段![]() 与抛物线的交点坐标.
与抛物线的交点坐标.
【答案】(1)![]() 点坐标为
点坐标为![]() ,矩形
,矩形![]() 的最小值为
的最小值为![]() ;(2)交点坐标为(3+
;(2)交点坐标为(3+![]() ,﹣
,﹣![]() ),(3﹣
),(3﹣![]() ,﹣
,﹣![]() ),(1﹣
),(1﹣![]() ,
,![]() ),(1+
),(1+![]() ,
,![]() ).
).
【解析】
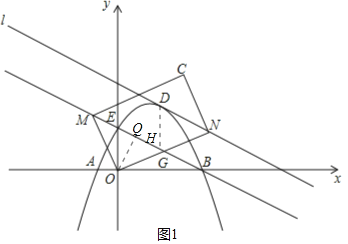
(1)当△DEB的面积最大时,直线DN与抛物线相切,可求出直线DN的解析式和点D的坐标,当矩形面积最小时,MG最小,求出MG的最小值即可.
(2)分两种情况讨论,以DB为边和以DB为对角线,分别求出此时ON的解析式,联立求出交点坐标即可.
解:(1)如图1所示,过点D作y轴的平行线交MB于点H,过点O作OQ垂直MB于点Q,
令y=0,解得x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
令x=0,y=2,
∴E(0,2),
设直线BE的解析式为y=kx+b,则![]()
解得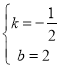 ,
,
∴直线BE的解析式为y=﹣![]() x+2,
x+2,
∵DN∥BE,
∴设直线DN的解析式为y=﹣![]() x+b1,
x+b1,
S△DEB=DH![]() (xB﹣xE),
(xB﹣xE),
∴当△DEB面积最大时,即是DH最大的时候,
∴﹣![]() x+b1=﹣
x+b1=﹣![]() x2+
x2+![]() x+2,
x+2,
△=b2﹣4ac=0,即16﹣4(2b1﹣4)=0,
解得b1=4,点D(2,3),
S矩=2S△MOG+S平形四边形,
∴矩形面积最小时就是MG最小,
设QG=m,MQ=n,
∴MG=m+n,
∵m+n≥2![]() ,
,
∵△QOG∽△MQO,
∴OQ2=mn,
∵△OEQ∽△EOB,
∴OQ=![]() ,
,
∴mn=![]() ,
,
∴m+n的最小值为![]() .
.
∴MG=![]() ,
,
∴S矩=2S△MOG+S平形四边形=![]() .
.
(2)分两种情况讨论,
情况一:当GN∥DB时,
直线DB的解析式为:y=﹣![]() x+6,
x+6,
则直线NG的解析式为y=﹣![]() x,
x,
∴﹣![]() x=﹣
x=﹣![]() x2+
x2+![]() x+2,
x+2,
解得x1=3+![]() ,x2=3﹣
,x2=3﹣![]() ,
,
∴交点坐标为(3+![]() ,﹣
,﹣![]() ),(3﹣
),(3﹣![]() ,﹣
,﹣![]() ),
),
情况二:DB为对角线时,此时NG必过DB的中点(3,![]() ),
),
设直线ON的解析式为y=k1x,
则k1=![]() ,
,
∴直线OD的解析式为y=![]() x,
x,
![]() =﹣
=﹣![]() x2+
x2+![]() x+2,
x+2,
解得x1=1﹣![]() ,x2=1+
,x2=1+![]() ,
,
∴交点坐标为(1﹣![]() ,
,![]() ),(1+
),(1+![]() ,
,![]() ),
),
综上所述:交点坐标为(3+![]() ,﹣
,﹣![]() ),(3﹣
),(3﹣![]() ,﹣
,﹣![]() ),(1﹣
),(1﹣![]() ,
,![]() ),(1+
),(1+![]() ,
,![]() ).
).


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
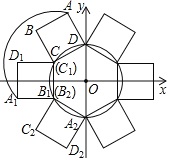
【题目】如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2)B.(2+![]() ,﹣1)
,﹣1)
C.(﹣1﹣![]() ,﹣1﹣
,﹣1﹣![]() )D.(1,﹣2﹣
)D.(1,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:已知二次函数![]() 经过点
经过点![]() .
.
(1)求该函数的表达式;
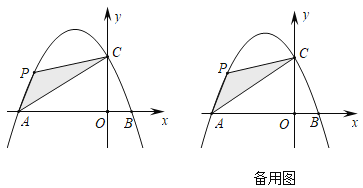
(2)如图所示,点![]() 是抛物线上在第二象限内的一个动点,且点
是抛物线上在第二象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标.
的坐标.
拓展:在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个不同的交点,请直接写出
有两个不同的交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,已知
,已知![]() .
.
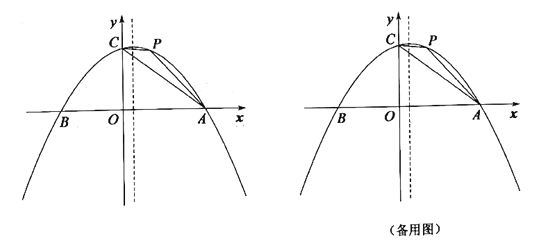
(1)点![]() 的坐标是______;
的坐标是______;
(2)若点![]() 是抛物线上的任意一点,连接
是抛物线上的任意一点,连接![]() 、
、![]() .
.
①当![]() 与
与![]() 的面积相等时,求点
的面积相等时,求点![]() 的坐标;
的坐标;
②把![]() 沿着
沿着![]() 翻折,若点
翻折,若点![]() 与抛物线对称轴上的点
与抛物线对称轴上的点![]() 重合,直接写出点
重合,直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体育考试时间越来越近,某校想了解初三年级1500名学生跳绳情况,从中随机抽查了20名男生和20名女生的跳绳成绩,收集到了以下数据:
男生:192、166,189,186,184,182,178,177,174,170,188,168,205,165,158,150,188,172,180,188
女生:186,198,162,192,188,186,185,184,180,180,186,193,178,175,172,166,155,183,187,184.
根据统计数据制作了如下统计表:
个数x | 150≤x<170 | 170≤x<185 | 185≤x<190 | x≥190 |
男生 | 5 | 8 | 5 | 2 |
女生 | 3 | 8 | a | 3 |
两组数据的极差、平均数、中位数、众数如表所示:
极差 | 平均数 | 中位数 | 众数 | |
男生 | 55 | 178 | b | c |
女生 | 43 | 181 | 184 | 186 |
(1)请将上面两个表格补充完整:a=____,b=_____,c=_____;
(2)请根据抽样调查的数据估计该校初三年级学生中考跳绳成绩能得满分(185个及以上)的同学大约能有多少人?
(3)体育组的江老师看了表格数据后认为初三年级的女生跳绳成绩比男生好,请你结合统计数据,写出支持江老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮看到路边上有人设摊玩“有奖掷币”游戏,规则是交2元钱可以玩一次掷硬币游戏,每次同时掷两枚硬币,如果出现两枚硬币都正面朝上,奖金5元;如果是其他情况,则没有奖金(每枚硬币落地只有正面朝上和反面朝上两种情况).
(1)小亮应不应该玩?
(2)如果有100人,每人玩一次这种游戏,设摊者约获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=![]() 的图象相交于A(m,3
的图象相交于A(m,3![]() ),C两点,已知点B(2
),C两点,已知点B(2![]() ,2
,2![]() ),则k的值为( )
),则k的值为( )

A. 6B. ﹣6C. 6![]() D. ﹣6
D. ﹣6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.

在第![]() 个图形中有______个三角形(用含
个图形中有______个三角形(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com