
| 75 |
| 16 |
| 75 |
| 16 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 82+62 |
| 1 |
| 2 |
| AD |
| AC |
| DH |
| CB |
| 5 |
| 8 |
| DH |
| 6 |
| 15 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 15 |
| 4 |
| 75 |
| 16 |

| 25 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 4 |
| 75 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 75 |
| 4 |
| 75 |
| 16 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 82+62 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BC |
| AB |
| 8×6 |
| 10 |
| 24 |
| 5 |
| S△DGH |
| S△BDC |
| DM |
| CN |
| DM |
| CN |
| DM |
| CN |
| 1 |
| 2 |
| 3 | ||
|
| 1 |
| 2 |
| 24 |
| 5 |
| 75 |
| 16 |
| 1 |
| 2 |
| KN |
| BC |
| DK |
| AC |
| KN |
| 6 |
| 3 |
| 8 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 25 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 8 |
| 75 |
| 16 |


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
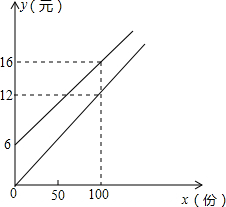 (2013•太原)某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(2013•太原)某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
(2013•太原)下表是我省11个地市5月份某日最高气温(℃)的统计结果:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com