
分析 解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,据此求解即可.
解答 解:方程两边同乘以x(x-1),得:3(x-1)-x2=-2x(x-1),
去括号,得:3x-3-x2=-2x2+2x,
移项,合并同类项,得:x2+x-3=0,
解得:x=$\frac{-1+\sqrt{13}}{2}$或x=-$\frac{1+\sqrt{13}}{2}$,
经检验x=$\frac{-1+\sqrt{13}}{2}$或x=-$\frac{1+\sqrt{13}}{2}$是原方程的解.
点评 此题主要考查了解分式方程的方法,要熟练掌握,解答此题的关键是要明确解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.


科目:初中数学 来源: 题型:解答题
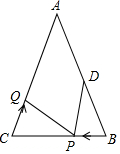 如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点,如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t<3).
如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点,如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t<3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
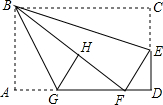 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
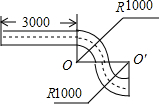 制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.右图是一段弯形管道,其中∠O=∠O’=90°,中心线的两条弧的半径都是1000mm,这段变形管道的展直长度约为(取π3.14)( )
制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.右图是一段弯形管道,其中∠O=∠O’=90°,中心线的两条弧的半径都是1000mm,这段变形管道的展直长度约为(取π3.14)( )| A. | 9280mm | B. | 6280mm | C. | 6140mm | D. | 457mm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
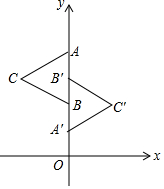 如图,正三角形ABC与正三角形A′B′C′关于某点成中心对称,已知A、B′、B三点的坐标分别是(0,4)、(0,3)、(0,2).
如图,正三角形ABC与正三角形A′B′C′关于某点成中心对称,已知A、B′、B三点的坐标分别是(0,4)、(0,3)、(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com