
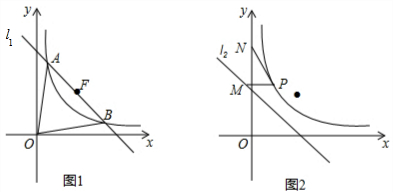
分析 (1)将l1与y=$\frac{1}{x}$组成方程组,即可得到C点坐标,从而求出△OAB的面积;
(2)根据题意得:$\left\{\begin{array}{l}y-\sqrt{2}=k(x-\sqrt{2})\\ y=\frac{1}{x}\end{array}\right.$ 整理得:kx2+$\sqrt{2}$(1-k)x-1=0(k<0),根据根与系数的关系得到2k2+5k+2=0,从而求出k的值;
(3)设P(x,$\frac{1}{x}$),则M(-$\frac{1}{x}$+$\sqrt{2}$,$\frac{1}{x}$),根据PM=PF,求出点P的坐标.
解答  解:(1)当k=-1时,l1:y=-x+2$\sqrt{2}$,
解:(1)当k=-1时,l1:y=-x+2$\sqrt{2}$,
联立得,$\left\{\begin{array}{l}y=-x+2\sqrt{2}\\ y=\frac{1}{x}\end{array}\right.$,化简得x2-2$\sqrt{2}$x+1=0,
解得:x1=$\sqrt{2}$-1,x2=$\sqrt{2}$+1,
设直线l1与y轴交于点C,则C(0,2$\sqrt{2}$).
S△OAB=S△AOC-S△BOC=$\frac{1}{2}$•2$\sqrt{2}$•(x2-x1)=2$\sqrt{2}$;
(2)根据题意得:$\left\{\begin{array}{l}y-\sqrt{2}=k(x-\sqrt{2})\\ y=\frac{1}{x}\end{array}\right.$ 整理得:kx2+$\sqrt{2}$(1-k)x-1=0(k<0),
∵△=[$\sqrt{2}$(1-k)]2-4×k×(-1)=2(1+k2)>0,
∴x1、x2 是方程的两根,
∴$\left\{\begin{array}{l}{x}_{1}+{x}_{2}=\frac{\sqrt{2}(k-1)}{k}\\{x}_{1}•{x}_{2}=-\frac{1}{k}\end{array}\right.$,
∴AB2=(x1-x2)2+($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)2
=(x1-x2)2+($\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$)2
=(x1-x2)2[1+($\frac{1}{{x}_{1}{x}_{2}}$)2]
=$\frac{2(1+{k}^{2})^{2}}{{k}^{2}}$,
∴AB=-$\frac{\sqrt{2}(1+{k}^{2})}{k}$=$\frac{5\sqrt{2}}{2}$,即$\frac{1+{k}^{2}}{k}$=$\frac{5}{2}$,
整理得,2k2+5k+2=0,即(2k+1)(k+2)=0,解得k=-2或k=-$\frac{1}{2}$.
(3)F($\sqrt{2}$,$\sqrt{2}$),如图:
设P(x,$\frac{1}{x}$),则M(-$\frac{1}{x}$+$\sqrt{2}$,$\frac{1}{x}$),
则PM=x+$\frac{1}{x}$-$\sqrt{2}$=$\sqrt{(x+\frac{1}{x}-\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}(x+\frac{1}{x})+4}$,
∵PF=$\sqrt{(x-\sqrt{2})^{2}+(\frac{1}{x}-\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}(x+\frac{1}{x})+4}$,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
当点P在NF上时等号成立,此时NF的方程为y=-x+2$\sqrt{2}$,
由(1)知P($\sqrt{2}$-1,$\sqrt{2}$+1),
∴当P($\sqrt{2}$-1,$\sqrt{2}$+1)时,PM+PN最小值是2.
点评 本题考查了反比例函数综合题,涉及函数图象的交点与方程组的解的关系、三角形的面积、一元二次方程根的判别式、一元二次方程的解法、两点间的距离公式的等知识,综合性较强.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
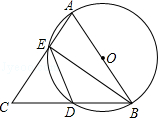 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 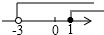 | B. | 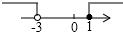 | C. |  | D. | 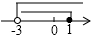 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
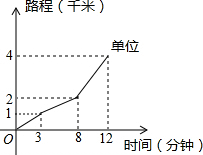 小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )
小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
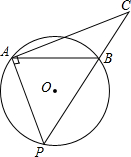 如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为8,$\frac{56}{15}$或$\frac{8\sqrt{5}}{3}$.
如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为8,$\frac{56}{15}$或$\frac{8\sqrt{5}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
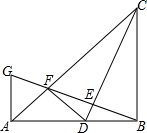 如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )
如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com