
【题目】在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如下表所示:
项目 | 购进数量(件) | 购进所需费用(元) | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 8300 |
第二次 | 40 | 30 | 6400 |
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
【答案】(1)酒精消毒液的进价为10元,测温枪的进价为200元;
(2)该公司销售完这1000件商品获得的最大利润为![]() 元.
元.
【解析】
(1)设酒精消毒液和测温枪每件的进价分别是![]() ,根据第一次购买30件酒精消毒液和40件测温枪的总费用为8300可以列出
,根据第一次购买30件酒精消毒液和40件测温枪的总费用为8300可以列出![]() ,根据第二次购买40件酒精消毒液和30件测温枪的总费用为6400可以列出
,根据第二次购买40件酒精消毒液和30件测温枪的总费用为6400可以列出![]() ,联立这两个方程即可求解;
,联立这两个方程即可求解;
(2)设购进酒精消毒液![]() 件,则购进测温枪
件,则购进测温枪![]() 件,销售完这1000件商品获得的利润为
件,销售完这1000件商品获得的利润为![]() ,根据酒精消毒液以每件20元出售,测温枪以每件240元出售,可以得到酒精消毒液每件的利润为10元,测温枪每件的利润为40元,由此可以求出利润的表达式;同时结合酒精消毒液的数量不少于测温枪数量的4倍列出不等式
,根据酒精消毒液以每件20元出售,测温枪以每件240元出售,可以得到酒精消毒液每件的利润为10元,测温枪每件的利润为40元,由此可以求出利润的表达式;同时结合酒精消毒液的数量不少于测温枪数量的4倍列出不等式![]() ,即可求出
,即可求出![]() 的取值范围,从而求出最大利润;
的取值范围,从而求出最大利润;
(1)设酒精消毒液和测温枪每件的进价分别是![]() 元,y元
元,y元
由题意可得:![]()
解得:![]()
![]() 酒精消毒液的进价为10元,测温枪的进价为200元
酒精消毒液的进价为10元,测温枪的进价为200元
(2)设购进酒精消毒液![]() 件,则购进测温枪
件,则购进测温枪![]() 件,销售完这1000件商品获得的利润为
件,销售完这1000件商品获得的利润为![]()
由题意可得:![]()
![]() 酒精消毒液的数量不少于测温枪数量的4倍
酒精消毒液的数量不少于测温枪数量的4倍
![]()
![]()
解得:![]()
![]() 利润
利润![]() 是关于
是关于![]() 的一次函数,同时
的一次函数,同时![]()
![]()
![]() 随着
随着![]() 的增大而减小
的增大而减小
![]() 当
当![]() 时,
时,![]() 有最大值为
有最大值为![]()
![]() 该公司销售完这1000件商品获得的最大利润为
该公司销售完这1000件商品获得的最大利润为![]() 元
元


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
整理、描述数据 按如下分组整理、描述这两组样本数据
个数 株数 大棚 |
|
|
|
|
|
|
甲 | 5 | 5 | 5 | 5 | 4 | 1 |
乙 | 2 | 4 | 6 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)
分析数据 两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 3047 |
乙 | 53 | 57 | 3022 |
得出结论:(1)估计乙大棚产量优秀的秧苗数为__________株;
(2)可以推断出__________大棚的小西红柿秧苗品种更适应市场需求,理由为_____________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
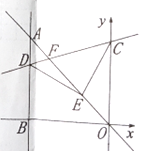
【题目】如图,在平面直角坐标系中,直线![]() 上一点
上一点![]() ,
,![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() ,线段
,线段![]() 绕点
绕点![]() 逆时针旋转90°至线段
逆时针旋转90°至线段![]() ,过点
,过点![]() 作直线
作直线![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,则点
,则点![]() 的坐标为(______)
的坐标为(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)B(-1,-2)两点,与![]() 轴相交于点C.
轴相交于点C.
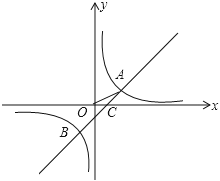
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | b | 7 | 5 | 8 | a | 8 | 7 |
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩表中的a= ,b= ;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为S甲2=0.81、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,第二轮结束时球又回到乙手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
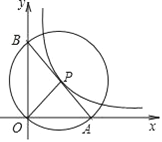
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com