
【题目】已知在等边三角形![]() 的三边上,分别取点
的三边上,分别取点![]() .
.
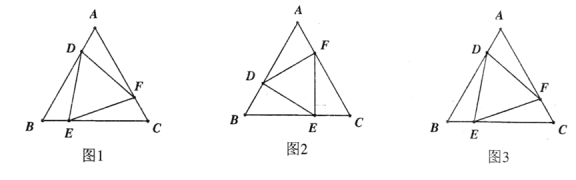
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 于点
于点![]() 于
于![]() 于
于![]() ,且
,且![]() ,求
,求![]() 的长;
的长;
(3)如图3,若![]() ,求证:
,求证:![]() 为等边三角形.
为等边三角形.
【答案】(1)证明见解析;(2)5;(3)证明见解析.
【解析】
(1)根据等边三角形的性质得出![]() ,
,![]() ,
,![]() ,进一步证得
,进一步证得![]() ,即可证得
,即可证得![]() ;
;
(2)根据等边三角形性质和30°的直角三角形性质,得出线段长之间关系,列出方程即可解答;
(3)延长BD到M,使BM=AD,连接ME,延长EC到N,使CN=BE,连接FN,可得![]() ,再证
,再证![]() ,从而得出
,从而得出![]() ,再由三角形外角性质即可证得结论.
,再由三角形外角性质即可证得结论.
证明:(1)如图1中,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
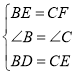 ,
,
∴![]() ,
,
(2)如图2中,![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
同理可得:![]() ,
,![]() ,
,
∵![]() ,即:
,即:![]()
∴![]()
解得:![]()
(3)如图3,延长BD到M,使BM=AD,连接ME,延长EC到N,使CN=BE,连接FN,
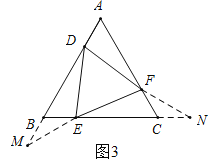
∵AD=CF,
∴BM=CF,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
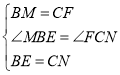 ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,
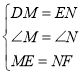 ,
,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ;
;
又∵![]()
∴![]() 为等边三角形.
为等边三角形.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米).
表示立方米).
每月用水量 | 单价 |
不超过 | 2元/ |
超出 | 4元/ |
超出 | 8元/ |
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水![]() ,则应收水费_________.元
,则应收水费_________.元
(2)若该户居民3月份用水![]() (其中
(其中![]() ),则应收水费多少元(用含a的代数式表示,并简化).
),则应收水费多少元(用含a的代数式表示,并简化).
(3)若该户居民4,5两个月共用水![]() (5月份用水量超过了4月份),设4月份,用水
(5月份用水量超过了4月份),设4月份,用水![]() ,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
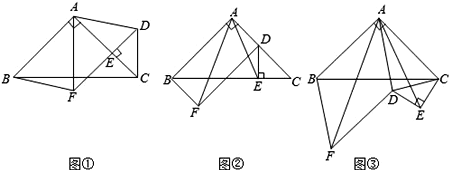
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
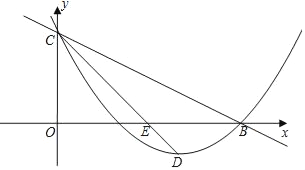
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“诗词大赛”预赛.参赛选手的成绩如下(单位:分)
九(1)班:88,91,92,93,93,93,94,98,99,100
九(2)班:89,93,93,93,95,96,96,96,98,99.
(1)九(2)班的平均分是 分;九(1)班的众数是 分;
(2)若从两个班成绩最高的5位同学中选2人参加市级比赛,则这两个人来自不同班级的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com