
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
【答案】
(1)
证明:连结OD,∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADE+∠BDO=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
又∵OD=OB,
∴∠B=∠BDO,
∴∠ADE=∠A.
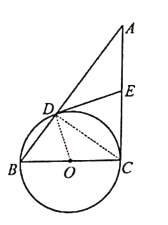
(2)
解:连结CD,∵∠ADE=∠A,
∴AE=DE,
∵BC是⊙O的直径,∠ACB=90°.
∴EC是⊙O的切线,∴DE=EC,
∴AE=EC.
又∵DE=10,
∴AC=2DE=20,
在Rt△ADC中,DC= ![]() .
.
设BD=x,
在Rt△BDC中,BC2=x2+122, 在Rt△ABC中,BC2=(x+16)2-202,
∴x2+122=(x+16)2-202,解得x=9,
∴BC= ![]() .
.

【解析】(1)连结OD,根据切线的性质和同圆的半径相等,及圆周角所对的圆周角为90°,得到相对应的角的关系,即可证明;(2)由(1)中的∠ADE=∠A可得AE=DE;由∠ACB=90°,可得EC是⊙O的切线,由切线长定理易得DE=EC,则AC=2DE,由勾股定理求出CD;设BD=x,再可由勾股定理BC2= x2+122=(x+16)2-202,可解出x的值,再重新代入原方程,即可求出BC.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )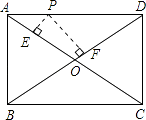
A.![]()
B.![]()
C.![]()
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】喜欢探究的亮亮同学拿出形状分别是长方形和正方形的两块纸片,其中长方形纸片的长为![]() ,宽为
,宽为![]() ,且两块纸片面积相等.
,且两块纸片面积相等.
(1)亮亮想知道正方形纸片的边长,请你帮他求出正方形纸片的边长;(结果保留根号)
(2)在长方形纸片上截出两个完整的正方形纸片,面积分别为![]() 和
和![]() ,亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积,所以一定能截出符合要求的正方形纸片来,你同意亮亮的见解吗?为什么?(参考数据:
,亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积,所以一定能截出符合要求的正方形纸片来,你同意亮亮的见解吗?为什么?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
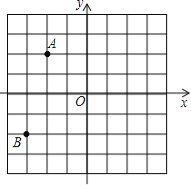
(1)若点C与点A关于原点O对称,则点C的坐标为 ;
(2)将点A向右平移5个单位得到点D,则点D的坐标为 ;
(3)由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
我们知道,“两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化的作用.
已知三角板![]() 中,
中,![]() ,长方形
,长方形![]() 中,
中,![]() .
.
问题初探:
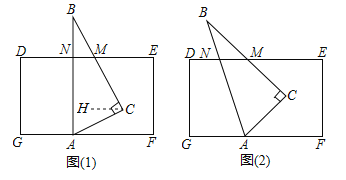
(1)如图(1),若将三角板![]() 的顶点
的顶点![]() 放在长方形的边
放在长方形的边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.
过点![]() 作
作![]() ,则有
,则有![]() ,从而得
,从而得![]() ,从而可以求得
,从而可以求得![]() 的度数.
的度数.
由分析得,请你直接写出:![]() 的度数为____________,
的度数为____________,![]() 的度数为___________.
的度数为___________.
类比再探:
(2)若将三角板![]() 按图(2)所示方式摆放(
按图(2)所示方式摆放(![]() 与
与![]() 不垂直),请你猜想写出
不垂直),请你猜想写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com