
【题目】七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用 水量x/m3 | 0< x≤5 | 5< x≤10 | 10< x≤15 | 15< x≤20 | x>20 |
频数/户数 | 12 | 20 | 3 | ||
百分比 | 12% | 7% |
若该小区有800户家庭,据此估计该小区月均用水量不超过10 m3的家庭有________户.
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:初中数学 来源: 题型:
【题目】(题文)图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.


![]() 图2的阴影部分的正方形的边长是______.
图2的阴影部分的正方形的边长是______.
![]() 用两种不同的方法求图中阴影部分的面积.
用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = ____________;
= ____________;
(方法2)![]() = ____________;
= ____________;
(3) 观察图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系;
![]() 根据
根据![]() 题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
①画出“基本图形”关于原点O对称的四边形A1B1C1D1 , 并填出A1 , B1 , C1 , D1的坐标;
②画出“基本图形”绕B点顺时针旋转90°所成的四边形A2B2C2D2
A1( , )B1( , )
C1( , )D1( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( ) 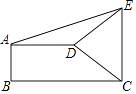
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )
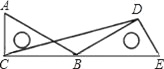
A. 4![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )
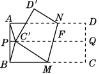
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com